FUNCIONES
Es decir, para todo y de Y se cumple que existe un único x de X , tal que la función evaluada en x es igual a y.
LÍMITES
lim fx) = L
x→a
lim fx) = L
x→a-
Una función f es una regla que asigna a cada elemento x de un conjunto D exacta-
mente un elemento, llamado f(x), de un conjunto E.
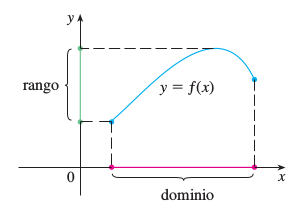
Usualmente consideramos funciones para los cuales los conjuntos D y E son conjuntos de números reales. Al conjunto D se le denomina dominio de la función. El número f(x) es el valor de f en x y se lee “f de x”. El rango de f es el conjunto de todos los valores posibles de f(x) conforme x varía a través de todo el dominio. Un símbolo que representa un número arbitrario en el dominio de una función f se llama variable independiente. Un símbolo que representa un número en el rango de f se conoce como variable dependiente.
Gráfica de una función
El método más común para la visualización de una función es su gráfica. Si f es una función con Dominio D entonces su gráfica es el conjunto de pares ordenados:
{(x, f(x) | x∈ D}
La gráfica de una función es una curva en el plano xy. Pero surge la pregunta: ¿qué curvas en el plano xy son gráficas de funciones? Esta pregunta se contesta con la siguiente
prueba.
La prueba de la vertical.
Una curva en el plano xy es la gráfica de una función de x si y sólo si no hay recta vertical que intercepte la curva más de una vez.
Esta es la gráfica de una función
No es la gráfica de una función
Simetría
Si una función f satisface f(-x) = f(x) para todo x en su dominio, entonces f es una función par.
Si f satisface f (-x) = -f(x) para cada x en su dominio, entonces f es una función impar.
Una función par
Funciones crecientes y decrecientes
La gráfica que se muestra sube desde A hasta B, desciende de B a C y sube otra vez de C a D. Se dice que la función f es creciente sobre el intervalo [a, b], decreciente sobre [b, c] y creciente nuevamente sobre [c, d]. Observe que si x1 y x2 son dos números entre a y b con x1<x2, entonces f(x1) < f(x2). Utilizamos esta propiedad para definir una función creciente.
Una función f se llama creciente sobre un intervalo I si
f(x1) < f(x2) siempre que x1 < x2 en I
Se llama decreciente sobre I si
f(x1) > f(x2) siempre que x1 < x2 en I
Igualdad de funciones
Dadas dos funciones, para que sean idénticas han de tener el mismo
dominio y codominio, y asignar la misma imagen a cada elemento del
dominio
Dadas dos funciones f : A → B y g : C → D, son iguales o idénticas si se cumple:
- Tienen el mismo dominio: A = C
- Tienen el mismo codominio: B = D
- Asignan las mismas imágenes: para cada x ∈ A = B, se tiene que f(x) = g(x)
- Tienen el mismo dominio: A = C
- Tienen el mismo codominio: B = D
- Asignan las mismas imágenes: para cada x ∈ A = B, se tiene que f(x) = g(x)
Función inyectiva
La función f: X → Y es inyectiva si, sólo si a, b son elementos de X tales que f(a)=f(b), entonces a=b
O equivalentemente , la función f: X → Y es inyectiva si, sólo si a, b son elementos diferentes de X, entonces f(a) ≠ f(b)
Simbólicamente,
∀ a,b ∈ X, f(a) = f(b) ⟹ a=b
que es equivalente a su contrarrecíproco
- ∀ a,b ∈ X, a ≠ b ⟹f(a) ≠ f(b)1
Para probar que una función no es inyectiva basta hallar dos valores
distintos del dominio, cuyas imágenes en el codominio son iguales.
Función suprayectiva
Im(f) = B
o, de modo equivalente, si todo elemento del codominio es la imagen de algún elemento del dominio:
Para cada b∈B existe un a∈A con f(a) =b
Función biyectiva
Una función es biyectiva si es al mismo tiempo inyectiva y sobreyectiva; es decir, si todos los elementos del conjunto de salida tienen una imagen distinta en el conjunto de llegada, y a cada elemento del conjunto de llegada le corresponde un elemento del conjunto de salida.
Formalmente, dada una función f:
f: X → Y
X → Y = f(x)
f: X → Y
X → Y = f(x)
La función es biyectiva si se cumple la siguiente condición:
∀ y ∈ Y : ∃! x ∈ X / f(x) = y
∀ y ∈ Y : ∃! x ∈ X / f(x) = y
Es decir, para todo y de Y se cumple que existe un único x de X , tal que la función evaluada en x es igual a y.
Dados dos conjuntos X e Y finitos, entonces existirá una biyección entre ambos si y sólo si X e Y tienen el mismo número de elementos y la función es inyectiva o sobreyectiva.
Prueba de la recta horizontal
Se ha estudiado cuando una ecuación en
x
y
y
define a
y
como función de
x.
x
como función de
y.
En este caso tenemos la función inversa de la primera.
No toda función definida a través de una ecuación tiene función inversa. El concepto de función
uno a uno (biunívoca, inyectiva) es clave para definir la función inversa de una función dada.
Se establece el criterio o prueba de la recta horizontal para determinar si la función es o no uno a uno.
Se propone una sucesión de pasos para obtener la inversa. La gráfica de la función inversa de f puede ser obtenida a partir de la gráfica de la función f reflejando esta última en la recta y = x.
Se establece el criterio o prueba de la recta horizontal para determinar si la función es o no uno a uno.
Se propone una sucesión de pasos para obtener la inversa. La gráfica de la función inversa de f puede ser obtenida a partir de la gráfica de la función f reflejando esta última en la recta y = x.
Una función es inyectiva si y sólo si ninguna línea horizontal intersecta su gráfica más de una vez.
Operaciones con funciones
Dadas las funciones f(x) y g(x) y a ∈ ℝ tenemos:
f+g(x) = f(x) + g(x)
f+g(x) = f(x) + g(x)
f-g(x) = f(x) - g(x)
f • g(x) = f(x) • g(x)
f/g(x) = f(x)/g(x) con g(x) diferente de cero
(a • f ) = a • f(x)
Composición de funciones
Una función compuesta es una función formada por la composición
o aplicación sucesiva de otras dos funciones. Para ello, se aplica
sobre el argumento la función más próxima al mismo, y al resultado del
cálculo anterior se le aplica finalmente la función restante.
Usando la notación matemática, la función compuesta g ∘ f: X → Z expresa que (g∘f)(x) = g(f(x)) para todo x perteneciente a X.
A g ∘ f se le llama composición de f y g. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
1. Definición
Supongamos que f(x) está definida cuando x está cerca del número a. (Esto significa que f está definida en algún intervalo abierto que contiene a a, excepto posiblemente en a misma.) Entonces escribimos
lim fx) = L
x→a
y decimos que “el límite de f(x), cuando x→a, es igual a L”
si podemos hacer que los valores de f(x) estén arbitrariamente cercanos a L (tan cercanos a L como queramos), tomando valores de x suficientemente cerca de a (por ambos lados de a), pero no iguales a a.
2. Definición
Cuando escribimos
lim fx) = L
x→a-
estamos diciendo que el límite izquierdo de f(x) cuando x se aproxima a a [o el límite de f(x) cuando x → a por la izquierda] es igual a L si podemos hacer que los valores de f(x) se acerquen arbitrariamente a L, tanto como queramos, tomando x suficientemente cercanos a a, pero menores que a.
Observe que la definición 2 difiere de la definición 1 sólo en el hecho de que x sea necesariamente menor que a. Del mismo modo, si se requiere que x sea mayor que a, se obtiene “el límite de f(x) cuando x→a por la derecha es igual a L” y escribimos. Así, el símbolo “x → a+” significa que se consideran sólo x > a.
Al comparar la definición 1 con las de los límites laterales, vemos que se cumple con lo siguiente.
3. Definición
3. Definición
lim fx) = L ⟺ lim fx) = L y lim fx) = L
x→a x→a- x→a+
4. Definición
Sea f una función definida por ambos lados de a, excepto posiblemente en la misma a. Entonces:
lim fx) = ∞
x→a
x→a
Significa que los valores de f(x) puedes ser arbitrariamente grandes (tan grandes como queramos) tomando x suficientemente cerca de a, pero no igual a a.
5. Definición
5. Definición
Sea f definida por ambos lados de a, excepto posiblemente en a misma, entonces:
lim fx) = -∞
x→a
Significa que los valores de f(x) puedes ser negativos arbitrariamente grandes tomando x suficientemente cerca de a, pero no igual a a.
6. Definición
La recta x = a se llama asíntota vertical de la curva y=f(x) si al menos una de las siguientes afirmaciones son verdaderas:
Suponga que c es una constante y que los límites
lim f(x) y lim g(x)
x→a x→a
existen. Entonces
Si f es una función polinomial o una función racional y a está en el dominio de f, entonces
Las funciones con la propiedad de sustitución directa se llaman continuas en x = a. Sin embargo, no todos los límites pueden ser evaluados por sustitución directa.
Igualdad de límites
Si f(x) = g(x) cuando x ≠ a, entonces
siempre que el límite exista
1.Teorema
lim fx) = L ⟺ lim fx) = L = lim fx)
x→a x→a- x→a+
2.Teorema
Si f(x) ≤ g(x) cuando x → a (excepto posiblemente en x = a) y los límites de f y g existen cuando x → a, entonces:
lim f(x) ≤ lim g(x)
x→a x→a
3.Teorema de la compresión
Si f(x) ≤ g(x) ≤ (h(x) cuando x⟶ a (excepto posiblemente en a) y
lim f(x) = lim h(x) = L
4.Teorema
Cualquier desigualdad permanece válida cuando la multiplicamos por un número positivo. Sabemos que x² ≥ 0 para toda x, así que multiplicando cada lado de la desigualdad por x² obtenemos:
Definición precisa de límite
Sea f la función definida sobre algún intervalo abierto que contiene el número a, excepto posiblemente en a misma. Entonces, decimos que el límite de f(x) cuando x tiene a a es L, y lo expresamos como
lim f(x) = L
x→a
si para cada número ε > 0 existe un número ઠ > 0 tal que
si 0 < | x - a| < ઠ entonces |f(x) - L| < ε
Definición de límite por la izquierda
x→a-
si para cada número 𝞮 > 0 existe un número 𝛿 > 0 tal que
si a - ઠ < x < a, entonces | f(x) - L| < ε
Definición de límite por la derecha
x→a+
si para cada número 𝞮 > 0 existe un número 𝛿 > 0 tal que
si a < x < a + ઠ, entonces | f(x) - L| < ε
La recta x = a se llama asíntota vertical de la curva y=f(x) si al menos una de las siguientes afirmaciones son verdaderas:
lim f(x) = ∞
x→a
lim f(x) = ∞
x→a-
lim f(x) = ∞
x→a+
lim f(x) = -∞
x→a
lim f(x) = -∞
x→a-
lim f(x) = -∞
x→a+
Cálculo de límites usando la Leyes de los límites:
Suponga que c es una constante y que los límites
lim f(x) y lim g(x)
x→a x→a
existen. Entonces
Si n es un numero entero positivo, entonces:
Si n es par, suponemos que:
Propiedad de sustitución directa.
lim f(x) > 0
x→aSi f es una función polinomial o una función racional y a está en el dominio de f, entonces
lim f(x) = f(a)
x→a
Las funciones con la propiedad de sustitución directa se llaman continuas en x = a. Sin embargo, no todos los límites pueden ser evaluados por sustitución directa.
Igualdad de límites
Si f(x) = g(x) cuando x ≠ a, entonces
lim f(x) = lim g(x)
x→a x→asiempre que el límite exista
1.Teorema
lim fx) = L ⟺ lim fx) = L = lim fx)
x→a x→a- x→a+
2.Teorema
Si f(x) ≤ g(x) cuando x → a (excepto posiblemente en x = a) y los límites de f y g existen cuando x → a, entonces:
lim f(x) ≤ lim g(x)
x→a x→a
Si f(x) ≤ g(x) ≤ (h(x) cuando x⟶ a (excepto posiblemente en a) y
lim f(x) = lim h(x) = L
x→a x→a
entonces
lim g(x) = L
x→a
El teorema de la compresión, llamado a veces teorema del Sándwich o del apretón. Se dice que si g(x) se comprime entre f(x) y h(x) cerca de a, y si f y h tienen el mismo límite L en a, entonces g es forzada a tener el mismo límite L en a.
El teorema de la compresión, llamado a veces teorema del Sándwich o del apretón. Se dice que si g(x) se comprime entre f(x) y h(x) cerca de a, y si f y h tienen el mismo límite L en a, entonces g es forzada a tener el mismo límite L en a.
4.Teorema
-1 ≤ sen 1/x ≤ 1
Cualquier desigualdad permanece válida cuando la multiplicamos por un número positivo. Sabemos que x² ≥ 0 para toda x, así que multiplicando cada lado de la desigualdad por x² obtenemos:
-x² ≤ x² sen 1/x ≤ x²
Sea f la función definida sobre algún intervalo abierto que contiene el número a, excepto posiblemente en a misma. Entonces, decimos que el límite de f(x) cuando x tiene a a es L, y lo expresamos como
lim f(x) = L
x→a
si para cada número ε > 0 existe un número ઠ > 0 tal que
si 0 < | x - a| < ઠ entonces |f(x) - L| < ε
La definición de límite señala que si cualquier
intervalo pequeño (L - ε, L + ε)
está dado alrededor de L, entonces podemos
encontrar un intervalo (a - ઠ, a + ઠ)
alrededor de a tal que f hace corresponder todos los puntos
de (a - ઠ, a + ઠ) (excepto
posiblemente en a) con los puntos del intervalo (L - ε, L + ε).
intervalo pequeño (L - ε, L + ε)
está dado alrededor de L, entonces podemos
encontrar un intervalo (a - ઠ, a + ઠ)
alrededor de a tal que f hace corresponder todos los puntos
de (a - ઠ, a + ઠ) (excepto
posiblemente en a) con los puntos del intervalo (L - ε, L + ε).
Definición de límite por la izquierda
lim f(x) = L
si a - ઠ < x < a, entonces | f(x) - L| < ε
Definición de límite por la derecha
lim f(x) = L
si a < x < a + ઠ, entonces | f(x) - L| < ε
CONTINUIDAD
En la sección anterior, hemos visto que el límite de una función cuando x tiende a a, con frecuencia se obtiene simplemente calculando el valor de la función en a. Las funciones con esta propiedad son llamadas continuas en x = a. Veremos que la definición matemática de continuidad coincide notoriamente con el sentido de continuidad que la palabra tiene en el lenguaje cotidiano. (Un proceso continuo es uno que se lleva a cabo gradualmente, sin interrupción o cambio brusco.)
Como se ilustra en la figura, si f es continua,
entonces los puntos (x, f (x)) en la gráfica
de f tienden al punto (a, f (a)) sobre la gráfica.
Así que no existe ninguna brecha en la curva.
Así que no existe ninguna brecha en la curva.
1.Definición
Una función f es continua en un número x = a si
El límite de f(x) cuando x⟶ a es igual a f(a)
Note que la definición 1 requiere implícitamente tres cosas. Si f es continua en a,
entonces:
1. f (a) está definida (esto es, a está en el dominio de f )
2. El límite de f(x) cuando x ⟶ a existe
3. El límite de f(x) cuando x ⟶ a es igual a f(a)
La definición indica que f es continua en a si f(x) tiende a f(a) cuando x⟶ a. Así, una función continua f tiene la propiedad de que un pequeño cambio en x produce sólo un pequeño cambio en f(x). De hecho, el cambio en f(x) puede mantenerse tan pequeño como se quiera manteniendo el cambio en x suficientemente pequeño.
Si f está definida cerca de a (en otras palabras, f está definida sobre un intervalo abierto que contiene a a, excepto quizás en a), decimos que f es discontinua en a (o f tiene una discontinuidad en a) si f no es continua en a.
Los fenómenos físicos son generalmente continuos. Por ejemplo, el desplazamiento o la velocidad de un vehículo varían continuamente con el tiempo, como lo hace la estatura de una persona. Pero hay otras situaciones, como la corriente eléctrica, donde ocurren discontinuidades.
Geométricamente, una función continua en cada número de un intervalo puede pensarse como una función cuya gráfica no tiene interrupciones. La gráfica puede dibujarse sin levantar la pluma del papel.
Una función f es continua por la derecha de un número x = a si
El limite de f(x) cuando x → a por la derecha (a+) = f(a)
y f es continua por la izquierda de x = a si
El limite de f(x) cuando x → a por la izquierda (a-) = f(a)
3. Definición
Una función f es continua sobre un intervalo si es continua en cada número en el intervalo. (Si f está definida sólo en un lado de un punto extremo del intervalo, entendemos por continua en el punto extremo, como continua por la derecha o continua por la izquierda.)
4. Teorema
Si f y g son continuas en x = a y x = c es una constante, entonces las
siguientes funciones son también continuas en x = a:
1 . f+g
2 . f-g
3 . cf
4. f ∙g
5. f/g si g(a) ≠ 0
5. Teorema
a) Cualquier función polinomial es continua en todo su dominio; es decir, es continua sobre ℝ (-∞, +∞)
b) Cualquier función racional es continua siempre que esté definida; esto es, es continua en su dominio.
Los siguientes tipos de funciones son continuas en todo número de sus dominios:
funciones polinomiales
funciones trigonométricas
funciones exponenciales
funciones racionales
funciones raíz
funciones trigonométricas inversas
funciones logarítmicas
8.Teorema
Si f es continua en b, y el límite de g(x) cuando x⟶ a es igual a b, entonces el límite de f(g(x)) cuando x⟶ a a es igual a f(b)
En otras palabras,
El límite de f(g(x)) cuando x⟶ a es igual al límite de f(límite de g(x) cuando x⟶ a)
Intuitivamente, el teorema es razonable porque si x está cerca de a, entonces g(x) está cerca de b, y como f es continua en b, si g(x) está cerca de b, entonces f (g(x)) está cerca de f(b).
Si g es continua en x = a y f es continua en g(a), entonces la función compuesta f o g dada por (f o g)(x) es igual a f(g(x)) es continua en x = a.
A menudo, este teorema se expresa de manera informal diciendo: “una función continua de una función continua es una función continua”.
10. Teorema del valor intermedio
Suponga que f es continua sobre el intervalo cerrado [a, b] y sea N cualquier número entre f(a) y f(b), donde f(a) es diferente de f(b). Entonces existe un número c en (a, b) tal que f(c) = N.
En esencia, el teorema dice que dada cualquier función f continua en el intervalo [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es paralela a la recta secante que une los puntos (b, f(b)) y (a, f(a)). Es decir:
El teorema del valor medio de Lagrange, de hecho, es una generalización del teorema de Rolle, que dice que si una función es definida y continua [a, b], diferenciable en el intervalo abierto (a, b), y toma valores iguales en los extremos del intervalo – en otras palabras, f(a) = f(b) – entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es horizontal, es decir f'(c) = 0.
Límites de las funciones TrigonométricasTeoremas:
lim sent = 0
Δt→0
lim cost = 0
lim sent/t = 1
lim 1-cost/t = 0
Δt→0
Δt→0
Demostración:
(1-cost) / t ∙ (1+cost)/(1+cost)
= (1-cos²t) / t(1+cost)
= (sen²t) / t(1+cost)
= (sent / t) ∙ sent/(1+cost)
⟹
lim 1-cost/t = 0
lim sent/t • lim sent/(1+cost)
= (1)(0/1+1) = 0
Tangentes
Si una curva tiene la ecuación y =f(x) y quiere usted hallar la recta tangente a la curva C en el punto P(a, f(a)), entonces considere un punto cercano Q(x,f(x)) donde x ≠ a y calcule la pendiente de la recta secante PQ:
Después, acerque Q a P a lo largo de la curva C, haciendo que x ⟶a. Si mPQ tiende a un número m, entonces definimos la tangente t como la recta que pasa por P con pendiente m. Esto equivale a decir que la recta tangente es la posición límite de la recta secante PQ cuando Q tiene a P.
1. Definición
La recta tangente a la curva y = f(x) en el punto P(a, f (a)) es la recta que pasa por P con
pendiente
pendiente
siempre que este límite exista.
2. Definición
Note que conforme x⟶ a, h se acerca a 0 (puesto que h = x - a y, por ende, la expresión de la pendiente de la recta tangente, en la definición anterior se convierte en:
La derivada de una función f en un número x = a, denotada por f '(a), es
si este límite existe
La recta tangente a y = f (x) en (a, f (a)) es la recta que pasa por (a, f (a)) cuya pendiente es igual a f '(a), la derivada de f en x = a.
Si utilizamos la forma punto-pendiente de la ecuación de la recta, podemos escribir la ecuación de la recta tangente a la curva y = f (x) en el punto (a, f (a)):
Otras notaciones
Si usamos la notación tradicional y=f(x) para indicar que la variable independiente es x y la dependiente es y, entonces algunas otras notaciones comunes para la derivada son:
Los símbolos D y d/dx se llaman operadores de derivación porque indican la operación de derivación, que es el proceso de calcular una derivada.
El símbolo dy/dx, introducido por Leibniz, no debe considerarse como una razón (por ahora); es sencillamente un sinónimo de f ' =(x). No obstante, es una notación útil y sugerente, en especial cuando se usa en la notación de incrementos. Se puede volver a escribir la definición de derivada en la notación de Leibniz en la forma:
Si desea indicar el valor de una derivada dy/dx en la notación de Leibniz en un número específico x = a, use la notación
que es un sinónimo para f ' (a).
Definición
Una función f es derivable en x=a si f '(a) existe. Es derivable sobre un intervalo abierto (a,b) [o (a,∞ ) o (-∞ , a) o (-∞ , ∞)] si es derivable en todo número del intervalo.
Teorema
Si f es derivable en x = a, entonces f es continua en x = a.
El inverso de este teorema es falso, es decir, hay funciones que son continuas, pero que no son derivables.
¿Cómo deja de ser derivable una función?
En general, si la gráfica de una función f tiene “esquinas” o “picos”, la gráfica de f no tiene recta tangente en esos puntos y f no es derivable allí. [Al intentar calcular f' a), encontramos que los limites por la izquierda y por la derecha son diferentes.]
Ejemplos de funciones no derivables en el punto a
Derivadas superiores
Si f es una función derivable, entonces su derivada f ' también es una función, así que f '
puede tener una derivada de sí misma, señalada por (f ') ' = f ''. Esta nueva función f '' se
denomina segunda derivada de f porque es la derivada de la derivada de f. Utilizando la
notación de Leibniz, la segunda derivada de y = f (x) se escribe como
Derivada de una función constante
Función constante
Regla de la potencia
Si n ∈ℝ entonces:
Si c es una constante
Regla de la suma: Si f y g son derivables, entonces:
Regla del múltiplo constante
Regla de la suma
si f y g son derivables, entonces
Regla de la resta
Si tanto f como g son derivables, entonces
Derivada de la función exponencial natural
Regla del producto
Regla del cociente
Si f y g son derivables, entonces
Formulas de derivación
Derivadas de las funciones trigonométricas
Regla de la cadena:
Si g es derivable en x y f es deribable en g(x), entonces la función compuesta F= fog definida mediante F(x) = f(g(x) es derivable en x y F' está dada por el producto
En la notación Leibniz, si y= f(u) y u = g(x) son funciones derivables, entonces
Regla de la potencia combinada conla regla de la cadena
Si n es cualquier número real y u = g(x) es derivable, entonces
de modo alternativo:
Derivadas de funciones logarítmicas
Si en la fórmula 1 ponemos a = e, entonces el factor ln a en el lado derecho se convierte en ln e = 1 y se obtiene la fórmula para la derivada de la función logarítmica natural
log ₑ x = ln x:
Pasos en la derivación logarítmica
Si f(x)<0 para algunos valores de x, entonces lnf(x) no está definida, pero podemos escribir |y| = |f(x)| y utilizar la ecuación Anterior. Este procedimiento se ilustra demostrando la versión general de la regla de la potencia.
DERIVADA
La derivada de una función f en un número x = a, denotada por f '(a), es
si este límite existe
La recta tangente a y = f (x) en (a, f (a)) es la recta que pasa por (a, f (a)) cuya pendiente es igual a f '(a), la derivada de f en x = a.
Si utilizamos la forma punto-pendiente de la ecuación de la recta, podemos escribir la ecuación de la recta tangente a la curva y = f (x) en el punto (a, f (a)):
y - f(a) = f '(a)(x - a)
Otras notaciones
Si usamos la notación tradicional y=f(x) para indicar que la variable independiente es x y la dependiente es y, entonces algunas otras notaciones comunes para la derivada son:
Los símbolos D y d/dx se llaman operadores de derivación porque indican la operación de derivación, que es el proceso de calcular una derivada.
El símbolo dy/dx, introducido por Leibniz, no debe considerarse como una razón (por ahora); es sencillamente un sinónimo de f ' =(x). No obstante, es una notación útil y sugerente, en especial cuando se usa en la notación de incrementos. Se puede volver a escribir la definición de derivada en la notación de Leibniz en la forma:
Si desea indicar el valor de una derivada dy/dx en la notación de Leibniz en un número específico x = a, use la notación
que es un sinónimo para f ' (a).
Definición
Una función f es derivable en x=a si f '(a) existe. Es derivable sobre un intervalo abierto (a,b) [o (a,∞ ) o (-∞ , a) o (-∞ , ∞)] si es derivable en todo número del intervalo.
Teorema
Si f es derivable en x = a, entonces f es continua en x = a.
El inverso de este teorema es falso, es decir, hay funciones que son continuas, pero que no son derivables.
¿Cómo deja de ser derivable una función?
En general, si la gráfica de una función f tiene “esquinas” o “picos”, la gráfica de f no tiene recta tangente en esos puntos y f no es derivable allí. [Al intentar calcular f' a), encontramos que los limites por la izquierda y por la derecha son diferentes.]
Ejemplos de funciones no derivables en el punto a
Derivadas superiores
Si f es una función derivable, entonces su derivada f ' también es una función, así que f '
puede tener una derivada de sí misma, señalada por (f ') ' = f ''. Esta nueva función f '' se
denomina segunda derivada de f porque es la derivada de la derivada de f. Utilizando la
notación de Leibniz, la segunda derivada de y = f (x) se escribe como
Derivada de una función constante
Función constante
Regla de la potencia
Si n ∈ℝ entonces:
Regla del múltiplo constante
Si C es una contante y f es una función derivable, entonces
Regla de la suma
si f y g son derivables, entonces
Regla de la resta
Si tanto f como g son derivables, entonces
Derivada de la función exponencial natural
Regla del producto
Regla del cociente
Si f y g son derivables, entonces
Formulas de derivación
Derivadas de las funciones trigonométricas
Regla de la cadena:
Si g es derivable en x y f es deribable en g(x), entonces la función compuesta F= fog definida mediante F(x) = f(g(x) es derivable en x y F' está dada por el producto
F'(x) = f'(g(x)) ∙g'(x)
En la notación Leibniz, si y= f(u) y u = g(x) son funciones derivables, entonces
Si n es cualquier número real y u = g(x) es derivable, entonces
de modo alternativo:
Podemos aplicar la regla de la cadena para derivar una función exponencial con cualquier base a > 0.
Porque ln a es una constante. En consecuencia, tenemos las fórmula
Derivada de las funciones trigonométrica inversas
Derivadas de funciones logarítmicas
Si en la fórmula 1 ponemos a = e, entonces el factor ln a en el lado derecho se convierte en ln e = 1 y se obtiene la fórmula para la derivada de la función logarítmica natural
log ₑ x = ln x:
Pasos en la derivación logarítmica
- 1. Tomar logaritmos naturales de ambos lados de una ecuación y=f(x) y utilizar las leyes de los logaritmos para simplificar.
- 2. Derivar implícitamente respecto a x
- 3. Resolver la ecuación resultante para y'
Si f(x)<0 para algunos valores de x, entonces lnf(x) no está definida, pero podemos escribir |y| = |f(x)| y utilizar la ecuación Anterior. Este procedimiento se ilustra demostrando la versión general de la regla de la potencia.






















































No hay comentarios.:
Publicar un comentario