1. Unidades fundamentales y unidades derivadas
El sistema SI está basado en siete unidades fundamentales (en ocasiones llamadas unidades base) y dos unidades complementarias. Todas las mediciones pueden ser expresadas como alguna combinación de unidades fundamentales y complementarias. La tabla 1 enumera las unidades fundamentales y la 2 las complementarias.
Tabla 1 y 2
La unidad eléctrica fundamental, el ampere, es la unidad utilizada para medir la corriente eléctrica. La corriente se abrevia con la letra I (por intensidad) y utiliza el símbolo A (por ampere). El ampere es único en el sentido de que utiliza en su definición a la unidad fundamental de tiempo (t) (el segundo). Todas las demás unidades eléctricas y magnéticas (tales como voltaje, potencia y flujo magnético) utilizan varias combinaciones de unidades fundamentales en sus definiciones y se llaman unidades derivadas.
Se utilizan símbolos literales para representar tanto cantidades como sus unidades. Se utiliza un símbolo para representar el nombre de la cantidad y otro para identificar la unidad de medición de dicha cantidad. Por ejemplo, P representa potencia y W watt, que es la unidad de potencia. Otro ejemplo es voltaje. En este caso, la misma letra representa tanto la cantidad como su unidad. La V cursiva representa el voltaje y la V recta el volt, el cual es la unidad de voltaje. Por lo general, las letras cursivas representan la cantidad y las rectas la unidad de dicha cantidad.
La tabla 3 enumera las cantidades eléctricas más importantes, junto con las unidades SI derivadas y sus símbolos. La tabla 4 enumera y relaciona las cantidades magnéticas, junto con las unidades SI derivadas y sus símbolos.
La tabla 3 enumera las cantidades eléctricas más importantes, junto con las unidades SI derivadas y sus símbolos. La tabla 4 enumera y relaciona las cantidades magnéticas, junto con las unidades SI derivadas y sus símbolos.
La notación científica
Proporciona un método conveniente para representar números grandes y pequeños y realizar cálculos que implican tales números. En notación científica, una cantidad se expresa como el producto de un número situado entre 1 y 10 y una potencia de diez. Por ejemplo, la cantidad 150,000 se expresa en notación científica como 1.5 10 5 , y la cantidad 0.00022 como 2.2 x 10⁴ .
Potencias de diez
La tabla 5 enumera algunas potencias de diez, tanto positivas como negativas, y los números decimales correspondientes. La potencia de diez se expresa como un exponente de la base 10 en cada caso (10^x ). Un exponente es un número al cual se eleva un número base. Indica la cantidad de lugares que el decimal se mueve hacia la derecha o a la izquierda para producir el número decimal.
Para una potencia positiva de diez, el punto decimal se mueve hacia la derecha para obtener el número decimal equivalente. Por ejemplo, para un exponente de 4,
10^4 = 1 * 10⁴ = 1.0000. = 10,000
Para una potencia negativa de diez, el punto decimal se mueve hacia la izquierda para obtener el número decimal equivalente. Por ejemplo, para un exponente de 4,
10^4 = 1 * 10⁴ = .0001. = 0.0001
Proporciona un método conveniente para representar números grandes y pequeños y realizar cálculos que implican tales números. En notación científica, una cantidad se expresa como el producto de un número situado entre 1 y 10 y una potencia de diez. Por ejemplo, la cantidad 150,000 se expresa en notación científica como 1.5 10 5 , y la cantidad 0.00022 como 2.2 x 10⁴ .
Potencias de diez
La tabla 5 enumera algunas potencias de diez, tanto positivas como negativas, y los números decimales correspondientes. La potencia de diez se expresa como un exponente de la base 10 en cada caso (10^x ). Un exponente es un número al cual se eleva un número base. Indica la cantidad de lugares que el decimal se mueve hacia la derecha o a la izquierda para producir el número decimal.
Para una potencia positiva de diez, el punto decimal se mueve hacia la derecha para obtener el número decimal equivalente. Por ejemplo, para un exponente de 4,
10^4 = 1 * 10⁴ = 1.0000. = 10,000
Para una potencia negativa de diez, el punto decimal se mueve hacia la izquierda para obtener el número decimal equivalente. Por ejemplo, para un exponente de 4,
10^4 = 1 * 10⁴ = .0001. = 0.0001
Notación de ingeniería
La notación de ingeniería es similar a la notación científica. Sin embargo, en notación de ingeniería un número puede tener de uno a tres dígitos a la izquierda del punto decimal y el exponente de potencia de diez debe ser un múltiplo de tres. Por ejemplo, el número 33,000 expresado en notación de ingeniería es 33 x10³ . En notación científica, se expresa como 3.3 x 10⁴ . Como otro ejemplo, el número 0.045 expresado en notación de ingeniería es 45 x 10³ . En notación científica, se expresa como 4.5 x 10² .
La notación de ingeniería es similar a la notación científica. Sin embargo, en notación de ingeniería un número puede tener de uno a tres dígitos a la izquierda del punto decimal y el exponente de potencia de diez debe ser un múltiplo de tres. Por ejemplo, el número 33,000 expresado en notación de ingeniería es 33 x10³ . En notación científica, se expresa como 3.3 x 10⁴ . Como otro ejemplo, el número 0.045 expresado en notación de ingeniería es 45 x 10³ . En notación científica, se expresa como 4.5 x 10² .
Prefijos métricos
En notación de ingeniería, los prefijos métricos representan cada una de las potencias de diez más comúnmente utilizadas. Estos prefijos métricos se enumeran en la tabla 6 junto con sus símbolos y potencias de diez correspondientes.
Se utilizan prefijos métricos sólo con números que tienen una unidad de medida, tal como volts, amperes y ohms, y preceden al símbolo de la unidad. Por ejemplo, 0.025 amperes puede ser expresada en notación de ingeniería como 25 x 10^⁻3 . Esta cantidad, expresada utilizando un prefijo métrico, es 25 mA, la cual se lee 25 miliamperes. Observe que el prefijo métrico mili ha reemplazado a 10^-3 . Como otro ejemplo, 100,000,000 ohms puede ser expresada como 100 x 10⁶ . Esta cantidad, expresada utilizando un prefijo métrico, es 100 Mohms, la cual se lee 100 mega ohms. El prefijo métrico mega ha reemplazado a 10⁶ .
En notación de ingeniería, los prefijos métricos representan cada una de las potencias de diez más comúnmente utilizadas. Estos prefijos métricos se enumeran en la tabla 6 junto con sus símbolos y potencias de diez correspondientes.
Tabla 6
Conversiones de unidades métricas
En ocasiones es necesario o conveniente convertir la cantidad de una unidad que tiene un prefijo métrico a otra, tal como de miliamperes (mA) a microamperes (uA). Recorriendo el punto decimal del número una cantidad apropiada de lugares hacia la izquierda o la derecha, según la conversión de que se trate, se obtiene la conversión de unidad métrica.
Las siguientes reglas básicas son aplicables a conversiones de unidades métricas:
1. Cuando se convierte una unidad grande en otra más pequeña, el punto decimal se mueve hacia la derecha.
2. Cuando se convierte una unidad pequeña en otra más grande, el punto decimal se mueve hacia la izquierda.
3. Se determina el número de lugares que debe recorrerse el punto decimal encontrando la diferencia en las potencias de diez de las unidades a convertir.
Por ejemplo, cuando se convierten miliamperes (mA) en microamperes ( uA), el punto decimal se recorre tres lugares hacia la derecha porque existe una diferencia de tres lugares entre las dos unidades (mA es 10^-3 A y uA es 10^-6 A).
2. Voltaje, Corriente y Resistencia
Carga Eléctrica [q,Q]
Nota:
q - varía en el tiempo
Q - constante en el tiempo
- Es una propiedad eléctrica de las partículas atómicas de las que se compone la materia.
- Su unidad de medida es el Coulomb (c).
- Hay dos clases de carga, la positiva y la negativa.
- Las cargas iguales se repelen, las cargas diferentes se atraen.
- La carga del electrón es negativa y de magnitud igual a 1.6021 x 10^⁻19 Coulombs, entonces en un Coulomb hay 6.24 x 10^18 electrones.
- La carga se da en múltiplos enteros de la carga electrónica (resultado experimental).
- La carga no se cre ni se destruye solo se transfiere.
Voltaje [v, V]
Como se ha visto, existe una fuerza de atracción entre una carga positiva y una negativa. Se debe aplicar cierta cantidad de energía, en forma de trabajo, para vencer dicha fuerza y separar las cargas a determinada distancia. Todas las cargas opuestas poseen cierta energía potencial a causa de la separación que hay entre ellas. La diferencia en la energía potencial por carga es la diferencia de potencial o voltaje. En circuitos eléctricos, el voltaje es la fuerza propulsora y es lo que establece la corriente.
Como una analogía, considere un tanque de agua que está soportado a varios pies sobre el nivel del suelo. Se debe ejercer una cantidad dada de energía, en forma de trabajo, para subir agua y llenar el tanque. Una vez almacenada en el tanque, el agua tiene cierta energía potencial que, si es liberada, puede utilizarse para realizar trabajo.
El voltaje, simbolizado mediante V, se define como energía o trabajo por unidad de carga.
V =W/Q
donde:
V = voltaje en volts (V)
W = energía en joules (J)
Q = carga en coulombs (C)
La unidad de voltaje es el volt, simbolizada mediante V. Un volt es la diferencia de potencial (voltaje) entre dos puntos cuando se utiliza un joule de energía para mover un coulomb de carga de un punto a otro.
Otra forma es la fuerza electromotriz (fem) externa que realiza el trabajo o transferencia de energía necesario para mover al electrón desde el punto a hasta el punto b.
Vab = dw /dq
Cuando se habla de voltaje o tensión, siempre están involucrados dos puntos, aún sin mencionar el segundo, uno de ellos es la referencia.
Vxy = voltaje de x con respecto a y
V1 = voltaje del punto 1 con respecto al punto de referencia.
Si Vab = Va-Vb
Se demuestra que Vab = -Vba
Vab = Va-Vb
= -Vb+Va
= - (Vb-Va)
= -Vba
Corriente [i, I]
El voltaje proporciona energía a los electrones, lo que les permite moverse por un circuito. Este movimiento de electrones es la corriente, la cual produce trabajo en un circuito eléctrico.
Como se ha aprendido, en todos los materiales conductores y semiconductores están disponibles electrones libres. Estos electrones se mueven al azar en todas direcciones, de un átomo a otro, dentro de la estructura del material.
El movimiento de estos electrones libres del extremo negativo del material al extremo positivo es la corriente eléctrica, simbolizada mediante I. La corriente eléctrica es la velocidad que lleva el flujo de la carga.
En un material conductor, el número de electrones (cantidad de carga) que fluyen más allá de cierto punto en una unidad de tiempo determinan la corriente.
I = Q/t
donde:
I = corriente en amperes (A)
Q = carga en coulombs (C)
t = tiempo en segundos (s)
Un ampere (1 A) es la cantidad de corriente que existe cuando cierto número de electrones, cuya carga total es de un coulomb (1 C), pasa por un área de sección transversal dada en un segundo (1 s).
El valor I de la intensidad instantánea será:
Si la intensidad permanece constante, en cuyo caso se denota Im, utilizando incrementos finitos de tiempo se puede definir como:
Si la intensidad es variable la fórmula anterior da el valor medio de la intensidad en el intervalo de tiempo considerado.
Corriente convencional vs corriente real
El sentido de la corriente eléctrica en un circuito eléctrico simboliza el sentido de los electrones a través del circuito.
Los electrones recorren una distancia de poco menos un milímetro en un segundo (dependiendo de la diferencia de potencial y el material por el que se propagan), mientras que la fuerza de propagación electromagnética, que es la que incita el movimiento de estos electrones es de 300.000 km/s (velocidad de la luz), desde la fuente generadora de tensión hasta el receptor para terminar en el polo contrario de la fuente suministradora de electricidad.
Existen dos formas de ver representada esta dirección del sentido de la corriente eléctrica, por un lado tenemos la forma de representar clásica o convencional. En la representación convencional la corriente se mueve desde el polo positivo hasta el polo negativo. Este sentido de la corriente no es real aunque en muchos documentos y explicaciones es así como se muestra.
La otra forma de representar el sentido de la corriente eléctrica es la representación real, la llamamos representación real porque es esa dirección y sentido la que tienen los electrones al circular por el circuito eléctrico.
Resistencia
Cuando en un material existe corriente, los electrones libres se mueven en éste y de vez en cuando chocan con átomos. Estas colisiones provocan que los electrones pierdan algo de su energía, con lo cual se restringe su movimiento. Entre más colisiones haya, más se restringe el flujo de electrones. Esta restricción varía y está determinada por el tipo de material. La propiedad de un material de restringir u oponerse al flujo de electrones se llama resistencia, R.
La resistencia es la oposición a la corriente. La resistencia se expresa en ohms, simbolizada mediante la letra griega omega (Ω).
Existe un ohm de resistencia si hay un ampere (1 A) de corriente en un material
cuando se aplica un volt (1 V) al material.
Para un conductor de tipo cable, la resistencia está dada por la siguiente fórmula:
Donde ρ es el coeficiente de proporcionalidad o la resistividad del material, l es la longitud del cable y S el área de la sección transversal del mismo.
La resistencia de un conductor depende directamente de dicho coeficiente, además es directamente proporcional a su longitud (aumenta conforme es mayor su longitud) y es inversamente proporcional a su sección transversal (disminuye conforme aumenta su grosor o sección transversal).
Resistores
Un componente diseñado específicamente para que tenga cierta cantidad de resistencia se llama resistor. La aplicación principal de los resistores es limitar la corriente en un circuito, dividir el voltaje, y, en ciertos casos, generar calor. Aun cuando los resistores vienen en muchas formas y tamaños, todos pueden ser colocados en dos categorías principales: fijos y variables.
Símbolo esquemático de resistencia:
Código de colores1
Artículo principal: Codificación de colores
Estos valores se indican con un conjunto de rayas de colores sobre el cuerpo del elemento. Son tres, cuatro o cinco rayas; dejando la raya de tolerancia (normalmente plateada o dorada) a la derecha, se leen de izquierda a derecha. La última raya indica la tolerancia (precisión). De las restantes, la última es el multiplicador y las otras indican las cifras significativas del valor de la resistencia.
El valor de la resistencia eléctrica se obtiene leyendo las cifras como un número de una, dos o tres cifras; se multiplica por el multiplicador y se obtiene el resultado en Ohmios (Ω). El coeficiente de temperatura únicamente se aplica en resistencias de alta precisión o tolerancia menor del 1%.
Como leer el valor de una resistencia
En una resistencia tenemos generalmente 4 líneas de colores, aunque podemos encontrar algunas que contenga 5 líneas (4 de colores y 1 que indica tolerancia). Vamos a tomar como ejemplo la más general, las de 4 líneas. Con la banda correspondiente a la tolerancia a la derecha, leemos las bandas restantes de izquierda a derecha, como sigue: Las primeras dos bandas conforman un número entero de dos cifras:- La primera línea representa el dígito de las decenas.
- La segunda línea representa el dígito de las unidades.
- La tercera línea representa la potencia de 10 por la cual se multiplica el número.
Por ejemplo:
- Observamos la primera línea: verde= 5
- Observamos la segunda línea: amarillo= 4
- Observamos la tercera línea: rojo= 2 o 100
- Unimos los valores de las primeras dos líneas y multiplicamos por el valor de la tercera
El recíproco de la resistencia es la conductancia, simbolizada mediante G. La conductancia es una medida de la facilidad con que se establece la corriente. La fórmula es:
G=1/R
La unidad de conductancia es el siemens, abreviada con S y su unidad es mho o una omega al reves.
El circuito eléctrico
Un circuito eléctrico básico es una agrupación ordenada de componentes físicos que utilizan voltaje, corriente y resistencia para realizar alguna función útil.
El diagrama esquemático de un circuito eléctrico Un circuito eléctrico puede ser representado mediante un diagrama esquemático que utiliza símbolos estándar para identificar cada elemento. Un diagrama esquemático muestra, de manera organizada, cómo están interconectados los diversos componentes de un circuito dado para que la operación del circuito pueda ser determinada.
Componentes de un circuito eléctrico
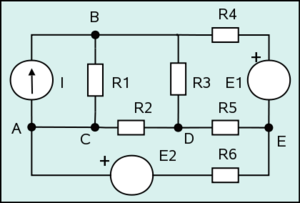
Figura: Circuito ejemplo.
- Componente: un dispositivo con dos o más terminales en el que puede fluir interiormente una carga. En la figura se ven 9 componentes entre resistores y fuentes.
- Nodo: punto de un circuito donde concurren más de dos conductores. A, B, C, D, E son nodos. C no se considera un nuevo nodo, porque se puede considerar el mismo nodo que A, ya que entre ellos no existe diferencia de potencial o tener tensión 0 (VA - VC = 0).
- Rama: porción del circuito comprendida entre dos nodos consecutivos. En la figura 1 hay siete ramales: AB por la fuente, BC por R1, AD, AE, BD, BE y DE. Obviamente, por un ramal solo puede circular una corriente.
- Malla: cualquier camino cerrado en un circuito eléctrico.
- Fuente: componente que se encarga de transformar algún tipo de energía en energía eléctrica. En el circuito de la figura hay tres fuentes: una de intensidad, I, y dos de tensión, E1 y E2.
- Conductor: comúnmente llamado cable, es un hilo de resistencia despreciable (idealmente cero) que une los elementos para formar el circuito.
Leyes fundamentales
Véase también: Análisis de circuitos
Las leyes fundamentales que rigen en cualquier circuito eléctrico son:- Ley de corriente de Kirchhoff: la suma de las corrientes que entran por un nodo debe ser igual a la suma de las corrientes que salen por ese nodo.
- Ley de tensiones de Kirchhoff: la suma de las tensiones en un lazo debe ser 0.
- Ley de Ohm: la tensión en una resistencia es igual al producto del valor de dicha resistencia por la corriente que fluye a través de ella.
- Teorema de Norton: cualquier red lineal que tenga una fuente de tensión o de corriente y al menos una resistencia es equivalente a una fuente ideal de corriente en paralelo con una resistencia.
- Teorema de Thévenin: cualquier red lineal que tenga una fuente de tensión o de corriente y al menos una resistencia es equivalente a una fuente ideal de tensión en serie con una resistencia.
- Teorema de superposición: en una red eléctrica lineal con varias fuentes independientes, la respuesta de una rama determinada cuando todas las fuentes están activas simultáneamente es igual a la suma lineal de las respuestas individuales tomando una fuente independiente a la vez.
3. Ley de Ohm
La ley de Ohm establece que la corriente es directamente proporcional al voltaje e inversamente proporcional a la resistencia, dada por la fórmula siguiente:
I = V/R
donde:
I = corriente en amperes (A)
V = voltaje en volts (V)
R = resistencia en ohms (Ω)
Con un valor constante de R, si el valor de V se incrementa, el valor de I se incrementa; si V disminuye, I disminuye. Si V se mantiene constante y R se incrementa, I disminuye. Asimismo, si V se mantiene constante y R disminuye, I se incrementa.
La diferencia de potencial (Vab) en los extremos de un resistor es directamente proporcional a la corriente que lo atraviesa. La constante de proporcionalidad es el valor de la resistencia del elemento.
Vab=RI
4. Energía y potencia
Energía es la capacidad de realizar trabajo, y potencia es la razón de cambio a la cual se utiliza la energía.
Potencia (P) es cierta cantidad de energía (W) utilizada en cierto tiempo (t) y expresada como sigue:
P =W/t
donde:
P = potencia en watts (W)
W = energía en joules (J)
t= tiempo en segundos (s)
Advierta que la W cursiva se utiliza para representar energía en la forma de trabajo y una W no cursiva representa watts, la unidad de potencia. El joule (J) es la unidad SI de energía.
La energía en joules dividida entre el tiempo en segundos da potencia en watts. Por ejemplo, si se utilizan 50 J de energía en 2 s, la potencia es de 50 J/2 s = 25 W. Por definición, Un watt (W) es la cantidad de potencia cuando se utiliza un joule en un segundo.
Por tanto, el número de joules utilizados en un segundo siempre es igual al número de watts. Por ejemplo, si se utilizan 75 J en 1 s, la potencia es P = W/t = 75 J/1 s = 75 W.
La potencia es la variación con respecto al tiempo de la entrega o absorción de la energía. Donde:
P=dw/dt =dw/dq * dq/dt => P=VI
Por convención:
- Si el elemento proporciona energía => la potencia es negativa P=VI<0 (la corriente sale del terminal positivo)
- Si el elemento consume energía => la potencia es positiva P=VI>0 (la corriente entra al terminal positivo)
Ley de la conservación de la energía
La suma de la potencia total en un circuito =0
Es decir:
La potencia proporcionada = La potencia consumida
La unidad de energía kilowatt-hora (kWh)
El joule ha sido definido como una unidad de energía. Sin embargo, existe otra forma de expresar la energía. Dado que la potencia se expresa en watts y el tiempo en segundos, se pueden utilizar unidades de energía llamadas watt-segundo (Ws), watt-hora (Wh), y kilowatt-hora (kWh).
Donde 1Wh = 3600 J
Donde 1Wh = 3600 J
Cuando paga su recibo de electricidad, le cobran con base en la cantidad de energía que utiliza, no la potencia. Como las compañías de electricidad comercian con enormes cantidades de energía, la unidad más práctica resulta ser el kilowatt-hora. Se cosume un kilowatt-hora de energía cuando se utilizan mil watts durante una hora. Por ejemplo, un foco de 100 W que permanezca encendido durante 10 h consume 1 kWh de energía.
W = Pt = (100 W)(10 h) = 1000 Wh = 1 kWh
Potencia en una resistencia
Cuando circula corriente a través de una resistencia, las colisiones de los electrones producen calor a consecuencia de la conversión de la energía eléctrica.
En un circuito eléctrico, la cantidad de potencia disipada depende de la cantidad de resistencia y de corriente, lo cual se expresa como sigue:
P = I²R
donde:
P = potencia en watts (W)
I = corriente en amperes (A)
R = resistencia en ohms (Ω)
Una expresión equivalente para potencia se obtiene, en función de voltaje y corriente, sustituyendo IR por V (I es I x I).
P = I² R = (I x I)R = I(IR) = (IR)I
P = VI
donde P está en watts cuando V está en volts e I está en amperes. Sustituyendo I por V/R (ley de Ohm) se obtiene otra expresión equivalente.
P = VI = V (V/R)
P =V²/R
La relación entre potencia y corriente, voltaje, y resistencia expresada en las fórmulas precedentes se conoce como ley de Watt. En cada caso, I debe estar en amperes, V en volts y R en ohms. Para calcular la potencia en una resistencia, se puede utilizar cualquiera de las tres fórmulas de potencia, según la información que se tenga. Por ejemplo, suponga que se conocen los valores de corriente y voltaje. En este caso, la potencia se calcula con la fórmula P= VI. Si se conocen I y R, se utiliza la fórmula P =I² R. Si V y R son los valores conocidos, se utiliza la fórmula P= V² /R.
5. Circuitos en Serie
Un circuito en serie proporciona sólo una trayectoria para el paso de la corriente entre dos puntos, de modo que la corriente es la misma a través de cada resistor en serie.
Elementos en serie -> comparten un sólo nodo que es exclusivo (Ningún otro elemento está conectado)
Corriente en un circuito en serie
En un circuito en serie, la corriente es la misma a través de todos los puntos. La corriente a través de cada resistor incluido en un circuito en serie es la misma corriente que pasa por todos los demás resistores que están en serie con él.
Resistencia total en serie
La resistencia total de un circuito en serie es igual a la suma de todas las resistencias de cada resistor individual dispuesto en serie.
Fórmula de la resistencia en serie
Para cualquier número de resistores individuales conectados en serie, la resistencia total es la suma de cada uno de los valores individuales.
RT = R1 + R2 + R3 +...+ Rn
donde RT es la resistencia total y Rn es el último resistor colocado en la serie (n puede ser cualquier entero positivo igual al número de resistores en serie).
Vs = V1 + V2 + V3 + ... + Vn
Como I es la corriente a través de cada uno de los resistores en serie, de acuerdo con la ley de Ohm, V1=R1*I , V2=R2*I , y así sucesivamente. Por sustitución en la ecuación para el voltaje,
Vs = R1*I + R2*I +R3*I + ... + Rn*I
Factorizando la corriente
Vs = I (R1+R2+R3+ ... + Rn)
Como Vs=I*RT
sustituyendo y eliminando I
I*RT = I (R1+R2+R3+ ... + Rn)
Vs = R1*I + R2*I +R3*I + ... + Rn*I
Factorizando la corriente
Vs = I (R1+R2+R3+ ... + Rn)
Como Vs=I*RT
sustituyendo y eliminando I
I*RT = I (R1+R2+R3+ ... + Rn)
tenemos que la resistencia total o equivalente es:
RT = R1+R2+R3+ ... + Rn
1. La corriente a través de cualesquiera resistores dispuestos en serie es la misma que la corriente total.
2. Cuando se conoce el voltaje total aplicado y la resistencia total, es posible determinar la corriente total por medio de la ley de Ohm.
IT =VT/RT
3. Cuando se conoce la caída de voltaje entre los extremos de uno de los resistores en serie (Rx ), es posible determinar la corriente total por medio de la ley de Ohm.
IT =Vx/Rx
4. Cuando se conoce la corriente total, es posible encontrar la caída de voltaje entre los extremos de cualquiera de los resistores en serie mediante la ley de Ohm.
VR = IT Rx
5. La polaridad de una caída de voltaje entre los extremos de un resistor es positiva en el extremo del resistor que está más cercano a la terminal positiva de la fuente de voltaje.
6. Se define que la corriente a través de un resistor circula en la dirección que va del extremo positivo del resistor al extremo negativo.
7. En un circuito en serie, una abertura impide el paso de la corriente; y, por consiguiente, existe una caída de voltaje igual a cero entre los extremos de cada resistor en serie. El voltaje total aparece entre los puntos donde está la abertura.
Potencia de circuitos en serie
La potencia disipada por cada resistor en un circuito dispuesto en serie contribuye a la potencia total presente en el circuito. Las potencias individuales son aditivas.
La cantidad total de potencia presente en un circuito resistivo dispuesto en serie es igual a la suma de potencias de cada resistor en serie.
PT = P1 + P2 + P3 + ... + Pn
donde PT es la potencia total y Pn es la potencia en el último resistor en serie.
Las fórmulas de potencia son aplicables a circuitos en serie. Como existe la misma corriente a través de cada resistor dispuesto en serie, se utilizan las fórmulas siguientes para calcular la potencia total:
P T = Vs I
P T = I² RT
PT =Vs²/RT
donde I es la corriente a través del circuito, Vs es el voltaje de fuente total de la conexión en serie, y RT es la resistencia total.
6. Circuitos en Paralelo
Resistores en paralelo
Cuando dos o más resistores se conectan individualmente entre dos puntos distintos, están en paralelo entre sí. Un circuito en paralelo proporciona más de una trayectoria para la corriente.
Una regla para identificar circuitos en paralelo es la siguiente:
Si existe más de una trayectoria (rama) para la corriente entre dos puntos distintos, y si el voltaje entre dichos puntos también aparece a través de cada una de las ramas, entonces existe un circuito en paralelo entre esos dos puntos.
Elementos en paralelo -> comparten los dos mismos nodos
Voltaje en un circuito en paralelo
El voltaje a través de cualquier rama de un circuito dispuesto en paralelo es igual al voltaje a través de cada una de las demás ramas en paralelo. Como ya se sabe, en un circuito en paralelo, cada trayectoria para la corriente se denomina rama.
Resistencia total en paralelo
Cuando se conectan resistores en paralelo, la resistencia total del circuito se reduce. La resistencia total de un circuito dispuesto en paralelo siempre es menor que el valor del resistor más pequeño. Por ejemplo, si un resistor de 10Ω y otro de 100Ω se conectan en paralelo, la resistencia total es menor que 10Ω.
Fórmula de la resistencia total en paralelo
El circuito mostrado en la figura ilustra un caso general de n resistores en paralelo (n puede ser cualquier número).
De acuerdo con la ley de las corrientes de Kirchhoff, la ecuación para corriente es
IT = I1 + I2 + I3 + ... + In
Como Vs es el voltaje a través de cada uno de los resistores en paralelo, de acuerdo con la ley de Ohm, I1=Vs/R1 , I2=Vs/R2 , y así sucesivamente. Por sustitución en la ecuación para corriente,
Vs/RT = Vs/R1 + Vs/R2 + Vs/R3 + ... + Vs/Rn
El término Vs puede ser factorizado en el lado derecho de la ecuación y se elimina con Vs del lado izquierdo, dejando únicamente los términos de resistencia.
1/RT = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn
Recuerde que el recíproco de la resistencia (1/R) se llama conductancia, la cual es simbolizada por G. La unidad de conductancia es el siemens (S)(o el mho). La ecuación para 1/RT puede ser expresada en función de la conductancia como
GT = G1 + G2 + G3 + ... + Gn
Resuelva para RT al tomar el recíproco de (es decir, invirtiendo) ambos lados de la ecuación para 1/R T .
RT = 1/(1/R1 + 1/R2 + 1/R3 + ... + 1/Rn)
La ecuación muestra que para determinar la resistencia total en paralelo, se suman todos los términos 1/R (o conductancia, G) y luego se toma el recíproco de la suma RT =1/GT
Potencia en circuitos en paralelo
La potencia total presente en un circuito en paralelo se encuentra sumando las potencias de todos los resistores individuales, tal como en los circuitos en serie.
La ecuación expresa la fórmula para determinar la potencia total en una forma concisa para cualquier cantidad de resistores dispuestos en paralelo,
PT = P1 + P2 + P3 + ... + Pn
donde PT es la potencia total y Pn es la potencia en el último resistor en paralelo. Como se puede ver, las potencias son aditivas, igual que en un circuito en serie.
Las fórmulas de potencia presentadas en el capítulo 4 son directamente aplicables a circuitos en paralelo.
7. Leyes de Kirchhoff
Ley de voltaje de Kirchhoff
La ley del voltaje de Kirchhoff es una ley fundamental de circuito que establece que la suma algebraica de todos los voltajes localizados en una sola trayectoria cerrada es cero o, en otras palabras, que la suma de las caídas de voltaje es igual al voltaje de fuente total.
En un circuito, la suma de todas las caídas de voltaje localizadas en una trayectoria cerrada única es igual al voltaje de fuente total encontrado en dicha espira.
El concepto general de la ley del voltaje de Kirchhoff
Vs = V1 + V2 + V3 + ... + Vn
donde el subíndice n representa el número de caídas de voltaje.
Al sumar todas las caídas de voltaje localizadas en una trayectoria cerrada y restar luego ese total al voltaje de fuente, el resultado es cero. Este resultado ocurre porque la suma de las caídas de voltaje siempre es igual al voltaje de la fuente.
La suma algebraica de todos los voltajes (tanto de fuente como de caídas) localizados en una trayectoria cerrada única es cero.
Por consiguiente, otra forma de expresar la ley del voltaje de Kirchhoff en forma de ecuación es:
Vs - V1 - V2 - V3 - ... - Vn = 0
Ley de las corrientes de Kirchhoff
La ley del voltaje de Kirchhoff se ocupa de los voltajes presentes en una sola trayectoria cerrada. La ley de la corriente de Kirchhoff es aplicable a corrientes que circulan por múltiples trayectorias.
La ley de las corrientes de Kirchhoff, abreviada a menudo como KCL, por sus siglas en inglés, puede ser enunciada como sigue:
La suma de las corrientes que entran a un nodo (corriente total de entrada) es igual a la suma de las corrientes que salen de dicho nodo (corriente total de salida).
Un nodo es cualquier punto o unión en un circuito donde dos o más componentes están conectados. En un circuito en paralelo, un nodo o unión es un punto donde se juntan las ramas dispuestas en paralelo.
una fórmula general de la ley de la corriente de Kirchhoff es
I ENTRADA(1) + I ENTRADA(2) + ... + I ENTRADA(n) = I SALIDA(1) + I SALIDA(2) + ... + I SALIDA(m)
Si todos los términos del lado derecho de la ecuación se pasan al lado izquierdo, sus signos cambian a negativos y en el lado derecho queda un cero como sigue:
I ENTRADA(1) + I ENTRADA(2) + ... + I ENTRADA(n) - I SALIDA(1) - I SALIDA(2) - ... - I SALIDA(m) = 0
La ecuación para corriente es por tanto:
IT = I1 + I2 + I3 + ... + In











No hay comentarios.:
Publicar un comentario