UNIDAD II Mediciones y Errores
Unidades de Longitud
Una pulgada de medida internacional mide exactamente 25,4 mm (por definición), mientras que una pulgada de agrimensor
de Estados Unidos se define para que 39,37 pulgadas sean exactamente un
metro. Para la mayoría de las aplicaciones, la diferencia es
insignificante (aproximadamente 3 mm por cada milla). La medida
internacional se utiliza en la mayoría de las aplicaciones para
agrimensura.
- 1 mil = 25,4 µm (micrómetros)
- 1 pulgada (in) = 1000 miles = 2,54 cm
- 1 pie (ft) = 12 in = 30,48 cm
- 1 yarda (yd) = 3 ft = 91,44 cm
- 1 rod (rd) = 5,5 yd = 5,0292 m
- 1 cadena (ch) = 4 rd = 20,1168 m
- 1 furlong (fur) = 10 ch = 201,168 m
- 1 milla (mi) = 8 fur = 1,609347 km
- 1 legua = 3 mi = 4,828032 km
- 1 link (li) = 7,92 in = 20,1168 cm
- 1 braza = 6 ft = 1,8288 m
Unidades de superficie
Las unidades de superficie en Estados Unidos se basan en la yarda cuadrada (sq yd o yd²).- 1 pulgada cuadrada (sq in o in²) = 6,4516 cm²
- 1 pie cuadrado (sq ft o ft²) = 144 in² = 929,0304 cm²
- 1 yarda cuadrada (sq yd o yd²) = 9 ft² = 0,83612736 m²
- 1 rod cuadrado (sq rd o ''rd²) = 30,25 yd² = 25,29285264 m²
- 1 rood = 40 rd² = 1011,7141056 m²
- 1 acre (ac) = 4 roods = 4046,8564224 m²
- 1 homestead = 160 ac = 64,7497027584 hm² (ha)
- 1 milla cuadrada (sq mi o mi²) = 4 homesteads = 2,589988110336 km²
- 1 legua cuadrada = 9 mi² = 23,309892993024 km²
Unidades de volumen
La "pulgada cúbica", el "pie cúbico" y la "yarda cúbica" se usan comúnmente para medir el volumen. Además existe un grupo de unidades para medir volúmenes de líquidos y otros.Además del pie cúbico, la pulgada cúbica y la yarda cúbica, estas unidades son diferentes a las unidades empleadas en el Sistema Imperial, aunque los nombres de las unidades son similares. Además, el sistema imperial no contempla más que un sólo juego de unidades tanto para materiales líquidos y secos. Hay muchas unidades con el mismo nombre y con la misma equivalencia (según el lugar), utilizados en partes del Reino Unido y de los Estados Unidos.8
En los Estados Unidos
Volumen para sólidos- 1 pulgada cúbica (in³ o cu in) = 16,387064 cm³ (ml)
- 1 pie cúbico (ft³ o cu ft) = 1728 in³ = 28,316846592 dm³ (l)
- 1 yarda cúbica (yd³ o cu yd) = 27 ft³ = 764,554857984 dm³ (l)
- 1 acre-pie = 1613,3 yd³ = 1,23348183754752 dam³ (Ml)
- 1 milla cúbica (mi³ o cu mi) = 3 379 200 acres-pie = 4,1681818254406 km³ (Tl)
- 1 pinta (pt) = 550,610471358 cm³ (ml)
- 1 cuarto (qt) = 2 pt = 1,10122094272 dm³ (l)
- 1 galón (gal) = 4 qt = 4,40488377086 dm³ (l)
- 1 peck (pk) = 2 gal = 8,80976754172 dm³ (l)
- 1 bushel (bu) = 4 pk = 35,2390701669 dm³ (l)
- 1 minim = 61,6115199219 μl (microlitros) (mm³)
- 1 dracma líquido (fl dr) = 60 minims = 3,69669119531 cm³ (ml)
- 1 onza líquida (fl oz) = 8 fl dr = 29,5735295625 cm³ (ml)
- 1 gill = 4 fl oz = 118,29411825 cm³ (ml)
- 1 pinta (pt) = 4 gills = 473,176473 cm³ (ml)
- 1 cuarto (qt) = 2 pt = 946,352946 cm³ (ml)
- 1 galón (gal) = 4 qt = 3,785411784 dm³ (l)
- 1 barril = 42 gal = 158,987294928 dm³ (l)
En el Reino Unido
Volumen para sólidos- 1 pulgada cúbica (in³ o cu in) = 16,387064 cm³ (ml)
- 1 pie cúbico (ft³ o cu ft) = 1728 in³ = 28,316846592 dm³ (l)
- 1 yarda cúbica (yd³ o cu yd) = 27 ft³ = 764,554857984 dm³ (l)
- 1 acre-pie = 1613,3 yd³ = 1,23348183754752 dam³ (Ml)
- 1 milla cúbica (mi³ o cu mi) = 3 379 200 acres-pie = 4,1681818254406 km³ (Tl)
- 1 cuarto (qt) = 1,32251120912 dm³ (l)
- 1 peck (pk) = 8 qt = 10,5800896729 dm³ (l)
- 1 bushel (bu) = 4 pk = 42,32035869184 dm³ (l)
- 1 minim = 59,19388388 μl μl (microlitros) (mm³)
- 1 escrúpulo líquido = 20 minims = 1,1838776776 cm³ (ml)
- 1 dracma líquido (fl dr) = 3 escrúpulos líquidos = 3,55163303281 cm³ (ml)
- 1 onza líquida (fl oz) = 8 fl dr = 28,4130642624 cm³ (ml)
- 1 gill = 5 fl oz = 142,065321312 cm³ (ml)
- 1 pinta (pt) = 4 gills = 568,261285248 cm³ (ml)
- 1 cuarto (qt) = 2 pt = 1,136522570496 dm³ (l)
- 1 galón (gal) = 4 qt = 4,546090281984 dm³ (l)
- 1 barril = 35 gal = 159,11315986944 dm³ (l)
Unidades de masa
Basada en el sistema avoirdupois, la unidad principal es la onza:- 1 grano (gr) = 64,79891 mg
- 1 dracma = 27,343749999961 gr = 1,771845195309973 g
- 1 onza (oz) = 16 dracmas = 28,34952312495957 g
- 1 libra (lb) = 16 oz = 453,5923699993531 g
- 1 stone (st) = 14 lb = 6,350293179990943 kg
- 1 arroba = 25 lb = (1,7857142857143 st) = 11,33980924998383 kg
- 1 quintal corto (US ctw) = 4 arrobas (100 lb) = 45,35923699993531 kg
- 1 quintal largo (UK ctw) = 8 st (112 lb) = 50,80234543992754 kg
- 1 cuarto corto (US qtr) = 5 US ctw (20 arrobas) = 226,7961849996766 kg
- 1 cuarto largo (UK qtr) = 5 UK ctw (40 st) = 254,0117271996377 kg
- 1 tonelada corta (US ton) = 4 US qtr (80 arrobas) = 907,1847399987064 kg
- 1 tonelada larga (UK ton) = 4 UK qtr (160 st) = 1016,046908798551 kg
Cifras significativas
Las cifras significativas representan el uso de una o más escalas de incertidumbre en determinadas aproximaciones.
Se dice que 4,7 tiene dos cifras significativas, mientras que 4,07
tiene tres. Para distinguir los llamados significativos de los que no
son, estos últimos suelen indicarse como potencias por ejemplo 5000 será
5x103 con una cifra significativa. También, cuando una
medida debe expresarse con determinado número de cifras significativas y
se tienen más cifras, deben seguirse las siguientes reglas:
- Primera: si se necesita expresar una medida con tres cifras significativas, a la tercera cifra se le incrementa un número si el que le sigue es mayor que 5 o si es 5 seguido de otras cifras diferentes de cero. Ejemplo: 53,6501 consta de 6 cifras y para escribirlo con 3 queda 53,7; aunque al 5 le sigue un cero, luego sigue un 1 por lo que no se puede considerar que al 5 le siga cero (01 no es igual a 0).
- Segunda: siguiendo el mismo ejemplo de tres cifras significativas: si la cuarta cifra es menor de 5, el tercer dígito se deja igual. Ejemplo: 53,649 consta de cinco cifras, como se necesitan 3 el 6 queda igual ya que la cifra que le sigue es menor de 5; por lo que queda 53,6.
- Tercera: cuando a la cifra a redondear le sigue 5 seguido solo de ceros, se considerará si la cifra a redondear es par o impar. Si la cifra a redondear es impar, ésta se incrementa en 1 dígito. Ejemplo: 12,35 se observa que el 3 que precede al 5 es impar, por tanto se incrementa en 1 cifra quedando 12,4. Si la cifra a redondear es par, ésta se deja igual. Ejemplo: 0,1865000 por ser el 6 par, se mantiene su valor y queda 0,186.
El uso de estas considera que el último dígito de aproximación es incierto, por ejemplo, al determinar el volumen de un líquido con una probeta cuya resolución es de 1mL,
implica una escala de incertidumbre de 0,5 mL. Así se puede decir que
el volumen de 6 mL será realmente de 5,5mL a 6,5mL. El volumen anterior
se representará entonces como (6,0 ± 0,5) mL. En caso de determinar
valores más próximos se tendrían que utilizar otros instrumentos de mayor resolución,
por ejemplo, una probeta de divisiones más finas y así obtener (6,0 ±
0,1) mL o algo más satisfactorio según la resolución requerida.
Una orden de magnitud es una
clase de escala o magnitud de cualquier cantidad, dónde cada clase
contiene valores de un cociente fijo con respecto a la clase precedente.
El cociente más comúnmente utilizado es el 10, puesto que, como hemos
visto, el sistema de medida utilizado en la actualidad es métrico
decimal. En Física es muy importante manejar los órdenes de magnitud, ya
que nos permiten representar y comparar de una forma simplificada las
distintas magnitudes físicas.
Los órdenes de magnitud se representan en notación científica, es decir, en potencias de 10.
Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.123
Si representamos el vector gráficamente podemos diferenciar la recta soporte o dirección, sobre la que se traza el vector.
Magnitudes Vectoriales
Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.
Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.5 6
Vector unitario
Es un vector de módulo uno. En ocasiones se le llama también vector normalizado. Con frecuencia resulta conveniente disponer de un vector unitario que tenga la misma dirección que un vector dado.


a = (ax, ay, az)
o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será:
a = axi + ayj + azk
Suma de vectores
La definición suma de vectores en el orden u+v produce otro vector, es como encadenar, siempre visualmente, un vector u y luego uno v. Diremos que u+v se simplifica como un vector w o que w descompone como suma de vectores u y v.

Método del paralelogramo
Este método permite solamente sumar vectores de dos en dos. Consiste
en disponer gráficamente los dos vectores de manera que los orígenes de
ambos coincidan en un punto, trazando rectas paralelas a cada uno de los
vectores, en el extremo del otro y de igual longitud, formando así un paralelogramo
(ver gráfico). El vector resultado de la suma es la diagonal de dicho
paralelogramo que parte del origen común de ambos vectores.
Partiendo de la representación gráfica del vector, sobre la misma
línea de su dirección tomamos tantas veces el módulo de vector como
indica el escalar.
Sean p un escalar y a un vector, el producto de p por a se representa pa y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es,
UNIDAD III Cinemática
Vectores
Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.123
Si representamos el vector gráficamente podemos diferenciar la recta soporte o dirección, sobre la que se traza el vector.
- El módulo o amplitud con una longitud proporcional al valor del vector.
- El sentido, indicado por la punta de flecha, siendo uno de los dos posibles sobre la recta soporte.
- El punto de aplicación que corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.
- El nombre o denominación es la letra, signo o secuencia de signos que define al vector.
Magnitudes Vectoriales
Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.
Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.5 6
Notación
Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flecha sobre la letra que designa su módulo (el cual es un escalar).Vector unitario
Es un vector de módulo uno. En ocasiones se le llama también vector normalizado. Con frecuencia resulta conveniente disponer de un vector unitario que tenga la misma dirección que un vector dado.
Representación gráfica de los vectores unitarios
Los vectores unitarios asociados con las direcciones de los ejes coordenados cartesianos x, y, z se designan por i, j, k, respectivamente.
Para hallar un vector unitario a partir de cualquier vector, hay que dividir este último por su módulo.
Vectores cartesianos
Son las componente rectangulares de un vector A dirigido dentro de un octante x,y,z mediante dos aplicaciones sucesivas del paralelogramos
Donde A = Ax +Ay +Az es la suma de los vectores componentes.
En coordenadas cartesianas, los vectores unitarios se representan por i, j, k, paralelos a los ejes de coordenadas x, y, z positivos.
Donde A = Ax +Ay +Az es la suma de los vectores componentes.
En coordenadas cartesianas, los vectores unitarios se representan por i, j, k, paralelos a los ejes de coordenadas x, y, z positivos.
A¯=Axi^+Ayj^+Azk^

A=A2x+A2y+A2z‾‾‾‾‾‾‾‾‾‾‾‾‾√
Magnitud de un vector cartesiano
A=A2x+A2y+A2z‾‾‾‾‾‾‾‾‾‾‾‾‾√
A=A2x+A2y+A2z‾‾‾‾‾‾‾‾‾‾‾‾‾√
Dirección de un vector cartesiano:

cosα=AxA
cosβ=AyA
cosγ=AzA
Podemos definir al vector por medio del vector unitario:
u^A=A¯A=AxAi^+AyAj^+AzAk^
El vector cartesiano quedaría definido como:
A¯=Au^A=Acosαi^+Acosβj^+Acosγk^
Componentes de un vector en el plano
La componente de un vector a lo largo de una línea en el espacio es su proyección sobre dicha línea. En un plano si A forma un ángulo θ con el eje x, sus componente x e y son:
Dirección de un vector cartesiano:
Podemos definir al vector por medio del vector unitario:
El vector cartesiano quedaría definido como:
Componentes de un vector en el plano
La componente de un vector a lo largo de una línea en el espacio es su proyección sobre dicha línea. En un plano si A forma un ángulo θ con el eje x, sus componente x e y son:
Ay = cateto opuesto / hipotenusa = A senθ
Donde el ángulo θ es la relación:
tanθ = Ay / Ax
= cateto opuesto /cateto adyacente
= senθ / cosθ
Módulo de un vector
|a| = √Ax² + Ay²
Componentes de un vector en el espacio
Las componente del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:
a = (ax, ay, az)
Ay = cateto opuesto / hipotenusa = A senθ
Donde el ángulo θ es la relación:
tanθ = Ay / Ax
= cateto opuesto /cateto adyacente
= senθ / cosθ
Módulo de un vector
Componentes de un vector en el espacio
Las componente del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:
o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será:
a = axi + ayj + azk
Suma de vectores
La definición suma de vectores en el orden u+v produce otro vector, es como encadenar, siempre visualmente, un vector u y luego uno v. Diremos que u+v se simplifica como un vector w o que w descompone como suma de vectores u y v.
Método del paralelogramo
Este método permite solamente sumar vectores de dos en dos. Consiste
en disponer gráficamente los dos vectores de manera que los orígenes de
ambos coincidan en un punto, trazando rectas paralelas a cada uno de los
vectores, en el extremo del otro y de igual longitud, formando así un paralelogramo
(ver gráfico). El vector resultado de la suma es la diagonal de dicho
paralelogramo que parte del origen común de ambos vectores.
Método del triángulo o método poligonal
Consiste en disponer gráficamente un vector a continuación de otro,
ordenadamente: el origen de cada uno de los vectores coincidirá con el
extremo del siguiente. El vector resultante es aquel cuyo origen
coincide con el del primer vector y termina en el extremo del último.
Método analítico para la suma y diferencia de vectores
Dados dos vectores libres,
a = axi + ayj + azk y b = bxi + byj + bzk
El resultado de su suma o de su diferencia se expresa en la forma
a+b = (axi + ayj + azk)+ (bxi + byj + bzk)
y ordenando las componentes,
a+b = (ax + bx)i + (ay + by)j + (az+ bz)k
Producto de un vector por un escalar
El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es igual a la del vector, y cuyo sentido es contrario a este si el escalar es negativo.
Sean p un escalar y a un vector, el producto de p por a se representa pa y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es,
pa = paxi + payj + pazk
Movimiento en una dimensión
Desplazamiento
El desplazamiento Δx de una partícula se define como su cambio de posición en algún intervalo de tiempo, conforme la partícula se mueve desde una posición inicial xi hasta una posición final xf su desplazamiento está dado por:
Δx = xf - xi
El desplazamiento es el área bajo la curva v en función de t.
La velocidad media en la dirección x, Vm se define como la razón entre el desplazamiento sobre el eje x y el intervalo de tiempo Δt.
En una gráfica de posición contra el tiempo, la velocidad media es la pendiente de la recta secante que pasa por los dos puntos.
Si se conocen las velocidades iniciales y finales del movimiento y la aceleración es constante, la velocidad media también se puede expresar como:
v
m=v₀+v₁
2
En este caso especial, estas expresiones dan el mismo resultado.
Módulo de la Velocidad media
El módulo de la velocidad media de una partícula es el cociente entre la distancia total recorrida y el tiempo total desde el principio al final del movimiento.
v
|v
m|= d
t
m|= d
t
La velocidad instantánea es el límite de la relación Δx / Δt cuando Δt se aproxima al valor cero y es la pendiente de la línea tangente a la curva x en función de t.
Este límite se denomina derivada de x respecto de t, la notación habitual es dx / dt
Vx(t) =lim∆t→0 ∆x
∆t= dx
dt
∆t= dx
dt
Esta pendiente puede ser positiva o negativa. En un movimiento unidimensional la velocidad instantánea puede ser positiva (x creciente) o negativa (x decreciente) o no hay movimiento. Un objeto que se mueve a velocidad constante, la velocidad instantánea coincide con la velocidad media.
Velocidad relativa
Si una partícula se mueve con velocidad vpA respecto a un sistema de coordenadas A, el cual a su vez se mueve con velocidad vAB respecto a otro sistema de coordenadas B, la velocidad de la partícula relativa a B es
vpB = vpA + vAB
Aceleración
= vv
t
La aceleración instantánea es el límite del cociente Δv / Δt cuando Δt tiende a cero. Si representamos la velocidad en función del tiempo, la aceleración instantánea en el tiempo t se define como la pendiente de la línea tangente a la curva en ese punto.
Este límite se denomina derivada de v respecto de t, la notación habitual es dv / dt
a =lim∆t→0 ∆v
∆t= dv
dt
∆t= dv
dt
Como la velocidad es también la derivada de la posición x respecto a t, la aceleración es la segunda derivada de x respecto a t, d²x/dt². Podemos ver el origen de esta notación escribiendo la aceleración como dv/dt y sustituyendo v por dx/dt:
a = dv
dt= d
dt ( dx/dt
dt )= d²x
dt²
dt= d
dt ( dx/dt
dt )= d²x
dt²
Si la aceleración es cero, no hay cambio de velocidad con el tiempo, es decir, la velocidad es constante. En este caso, la curva de x en función de t es una línea recta. Si la aceleración no es nula, pero constante, la velocidad varía linealmente con el tiempo y la curva de x en función de t es cuadrática con el tiempo.
Movimiento con aceleración constante
El movimiento de una partícula que tiene aceleración constante es corriente en la naturaleza. Por ejemplo, cerca de la superficie de la tierra todos los objetos caen verticalmente con aceleración de la gravedad constante (si puede despreciarse la resistencia del aire). (si una partícula tiene una aceleración constante a, su aceleración media en cualquier intervalo de tiempo es también a, Es decir,
m= a =∆v
∆ t
Si la velocidad es Vo en el tiempo t = 0 y v al cabo de cierto tiempo t, la aceleración correspondiente es
a = ∆v
∆t=v-v₀
t
∆t=v-v₀
t
Reajustando esta expresión se obtiene v en función de t.
v = v0 + at
El desplazamiento Δx = x - x0 en el intervalo de tiempo Δt = t - 0 es
Δx = vm Δt = vmt
Para una aceleración constante, la velocidad varía linealmente con el tiempo y la velocidad media es el valor medio de las velocidades inicial y final. (esta relación es válida sólo si la aceleración es constante.) Si V0 es la velocidad inical y V la velocidad final, la velocidad media es
v
m=v₀+v
2
m=v₀+v
2
El desplazamiento es, por lo tanto,
Δx = x - x0 = vmt = 1/2(v0+v)t
Podemos eliminar v sustituyendo v = v0 +at
Δx = 1/2(v0+v)t = 1/2(v0+v0+at)t = v0t + 1/2 at²
El desplazamiento es, así:
Δx = V0t + 1/2 at²
El término Vot representa el desplazamiento que tendría lugar si a fuera cero y el término 1/2at² es el desplazamiento adicional debido a la aceleración constante.
Eliminando t entre de las ecuaciones se obtiene
Δx = vmt = 1/2(v0+v)t = 1/2(v0+v) (v-v0)/a = (v²-v0²)/2a
es decir:
v² = v0² + 2aΔx
Ésta ecuación es útil, por ejemplo, si se trata de determinar la velocidad de una pelota que se ha dejado caer desde cierta altura x cuando no nos interesa conocer el tiempo de caída.
Movimiento en dos y tres dimensiones
Vector Desplazamiento
En mecánica, el desplazamiento es el vector que define la posición de un punto o partícula en relación a un origen A con respecto a una posición B. El vector se extiende desde el punto de referencia hasta la posición final. Cuando se habla del desplazamiento en el espacio solo importa la posición inicial y la posición final, ya que la trayectoria que se describe no es de importancia.
Δr = r2 - r1
En dos dimensiones:
Vector desplazamiento y distancia recorrida a lo largo de un camino.
En tres dimensiones:
El módulo del vector desplazamiento es inferior a la distancia recorrida a lo largo de la curva a menos que la partícula se mueva en línea recta.
Vector posición
El vector posición de una partícula es un vector trazado desde el origen de un sistema de coordenadas hasta la posición de la partícula.
Para una partícula en el punto (x, y) su vector posición r es
Para una partícula en el punto (x, y) su vector posición r es
r = xi + yj

Vector de posición de una partícula en el plano
Para una partícula en el punto (x, y,z) su vector posición r es
r = xi + yj + zj
Vector de posición de una partícula en el sistema de coordenadas cartesianas.
Velocidad media
La velocidad media se define como el cambio de posición durante un intervalo de tiempo considerado. Se calcula dividiendo el vector desplazamiento (Δr) entre el escalar tiempo (Δt) empleado en efectuarlo:
De acuerdo con esta definición, la velocidad media es una magnitud vectorial (ya que es el resultado de dividir un vector entre un escalar).
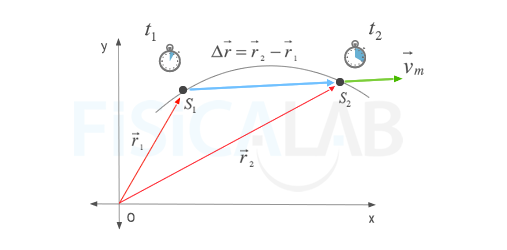
La velocidad media de un cuerpo (verde) es un vector que tiene la misma dirección y sentido que el vector desplazamiento (azul) y cuyo módulo es el cociente Δx / Δt entre el módulo de dicho vector y el tiempo transcurrido.
El módulo del vector velocidad media, en general, es diferente al valor de la velocidad media sobre la trayectoria. Solo serán iguales si la trayectoria es rectilínea y si el móvil solo avanza (en uno u otro sentido) sin retroceder.
Velocidad instantánea
Puede obtenerse una expresión para la velocidad instantánea en cualquier punto del recorrido, tomando el límite cuando el intervalo de tiempo se hace mas y mas pequeño. A ese proceso de tomar el límite se le llama derivación y la velocidad instantánea se puede definir como:
donde:
v→ : Vector velocidad instantánea.v→m : Vector velocidad media.∆r− : Vector desplazamiento.∆ t : Intervalo de tiempo que tiende a 0, es decir, un intervalo infinitamente pequeño.
Para calcular la derivada de la ecuación anterior expresamos el vector posición en función de sus componentes.
v = dx/dt i + dy/dt j +dz/dt k
= vxi + vyj+ vzk
= vxi + vyj+ vzk
Es el límite del vector aceleración media cuando Δt tiende a cero, que es igual al límite de la variación del vector velocidad instantánea Δv y el intervalo de tiempo Δt cuando el intervalo de tiempo se aproxima a cero; es decir, el vector aceleración instantánea es la derivada del vector velocidad respecto al tiempo:
v = dx/dt i + dy/dt j + dz/dtk = vxi + vyj + vzk
Por tanto,
a =dvx/dt i + dvy/dt j + dvz/dt k
=d²x/dt i + d²y/dt j + d²z/dt k
=axi + ayj + azk
Movimiento parabólico
Se denomina movimiento parabólico, al movimiento realizado por cualquier objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio
uniforme. El movimiento parabólico es un ejemplo de un movimiento
realizado por un objeto en dos dimensiones o sobre un plano. Puede
considerarse como la combinación de dos movimientos que son un
movimiento horizontal uniforme y un movimiento vertical acelerado.
En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico.
En la superficie de la Tierra, ese movimiento es tan parecido a una
parábola que perfectamente podemos calcular su trayectoria usando la
ecuación matemática de una parábola. La ecuación de una elipse es
bastante más compleja. Al lanzar una piedra al aire, la piedra intenta
realizar una elipse en uno de cuyos focos está el centro de la Tierra.
Al realizar esta elipse inmediatamente choca con el suelo y la piedra se
para, pero su trayectoria es en realidad un "trozo" de elipse. Es
cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de
parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos
"tiro parabólico". Si nos alejamos de la superficie de la Tierra sí
tendríamos que utilizar una elipse(como en el caso de los satélites
artificiales).
El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales (siempre que la altura de salida y de llegada sean iguales)
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
- Se puede analizar el movimiento en vertical independientemente del horizontal.
Tipos de movimiento parabólico
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
- El tiempo que tarda en alcanzar su altura máxima es el mismo tiempo que tarda en recorrer la mitad de su distancia horizontal, es decir, el tiempo total necesario para alcanzar la altura máxima y regresar al suelo es el mismo para el total de recorrido horizontal.
Las ecuaciones del lanzamiento horizontal son:
(Ec1) Las ecuaciones del m.r.u. para el eje x
(Ec2) Las ecuaciones del m.r.u.a. para el eje y
Tiro parabólico oblicuo
Hay dos ecuaciones que rigen el movimiento parabólico:
donde:
- es el módulo de la velocidad inicial.
- es el ángulo de la velocidad inicial sobre la horizontal.
- es la aceleración de la gravedad.
- son dos versores (vectores unitarios) en el plano.
- que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo v0x
- que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo v0y
Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:- a = -gj
Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
Ecuación de la posición
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
La trayectoria del movimiento parabólico está formada por la combinación de dos movimientos, uno horizontal de velocidad constante, y otro vertical uniformemente acelerado; la conjugación de los dos da como resultado una parábola.
0 sinθg
Alcance horizontal
El alcance horizontal de cada uno de los proyectiles se obtiene de:
0 sinθg
Su valor máximo se obtiene para el ángulo de disparo θ =90º.
Tiro parabólico con altura inicial.
Tiro parabólico con altura inicial.
Se dispara un proyectil desde una altura h sobre un plano horizontal con velocidad inicial v0, haciendo un ángulo θ con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura:
Las componentes de la velocidad del proyectil son:
v0x=v0·cosθ y v0y=v0·senθ
y en función del tiempo
y en función del tiempo
v0y=v0·senθ - gt
La posición del proyectil en función del tiempo es
x(t)= x0 + v0y·t
x(t)= x0 + v0y·t
y(t)= h+v0yt -12gt2
Estas son las ecuaciones paramétricas de la
trayectoria, ya que dado el tiempo t, se obtiene la posición x
e y del proyectil.
El tiempo de vuelo T
Haciendo y0=0 y despejando t (aplicando la formula para una ecuación de segundo grado) en y(t) tenemos:
Alcance máximo
Haciendo y0=0 y despejando t (aplicando la formula para una ecuación de segundo grado) en y(t) tenemos:
Sustituimos t en x = v0y·t nos queda
xmax = v0·senθ t
Velocidad final
La velocidad final y el ángulo que forma con el eje X
son (con z= gh/v0²)
xmax = v0·senθ t
Velocidad final
La velocidad final y el ángulo que forma con el eje X son (con z= gh/v0²)
La relación entre el ángulo de disparo θm
y el ángulo φm que forma el
vector velocidad cuando el proyectil llega al suelo es
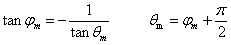
El vector velocidad inicial v0 y el
vector velocidad final vf son perpendiculares,
La relación entre el ángulo de disparo θm y el ángulo φm que forma el vector velocidad cuando el proyectil llega al suelo es
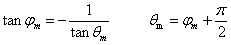
Tiro parabólico horizontal
Dado que, como dijimos anteriormente, la velocidad forma un ángulo α con la horizontal, las componentes x e y se determinan recurriendo a las relaciones trigonométricas más habituales:
Tiro parabólico horizontal
Dado que, como dijimos anteriormente, la velocidad forma un ángulo α con la horizontal, las componentes x e y se determinan recurriendo a las relaciones trigonométricas más habituales:
| Posición (m) | Velocidad (m/s) | Aceleración (m/s2) | |
|---|---|---|---|
| Eje Horizontal | |||
| Eje Vertical |

Movimiento circular
En el movimiento circular hay que tener en cuenta algunos conceptos básicos para la descripción cinemática y dinámica del mismo:
Arco angular o desplazamiento angular es el arco de la circunferencia recorrido por la masa puntual en su trayectoria circular, medido en radianes y representado con las letras griegas (phi) o (theta). Este arco es el desplazamiento efectuado en el movimiento circular y se obtiene mediante la posición angular ( ó ) en la que se encuentra en un momento determinado el móvil y al que se le asocia un ángulo determinado en radianes. Así el arco angular o desplazamiento angular se determinará por la variación de la posición angular entre dos momentos final e inicial concretos (dos posiciones distintas):
La aceleración angular es la variación de la velocidad angular por unidad de tiempo y se representa con la letra: y se la calcula:
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:
En cinemática, el movimiento circular (también llamado movimiento circunferencial) es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de giro es constante (giro ondulatorio), se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio, centro fijo y velocidad angular constante.
Conceptos
En el movimiento circular hay que tener en cuenta algunos conceptos básicos para la descripción cinemática y dinámica del mismo:
- Eje de giro: es la línea recta alrededor de la cual se realiza la rotación, este eje puede permanecer fijo o variar con el tiempo pero para cada instante concreto es el eje de la rotación (considerando en este caso una variación infinitesimal o diferencial de tiempo). El eje de giro define un punto llamado centro de giro de la trayectoria descrita (O).
- Arco: partiendo de un centro fijo o eje de giro fijo, es el espacio recorrido en la trayectoria circular o arco de radio unitario con el que se mide el desplazamiento angular. Su unidad es el radián (espacio recorrido dividido entre el radio de la trayectoria seguida, división de longitud entre longitud, adimensional por tanto).
- Velocidad angular: es la variación del desplazamiento angular por unidad de tiempo (omega minúscula, ).
- Aceleración angular: es la variación de la velocidad angular por unidad de tiempo (alfa minúscula, ).
En dinámica de los movimientos curvilíneos, circulares y/o giratorios se tienen en cuenta además las siguientes magnitudes:
- Momento angular (L): es la magnitud que en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento pero aplicada al movimiento curvilíneo, circular y/o giratorio (producto vectorial de la cantidad de movimiento por el vector posición, desde el centro de giro al punto donde se encuentra la masa puntual).
- Momento de inercia (I): es una cualidad de los cuerpos que depende de su forma y de la distribución de su masa y que resulta de multiplicar una porción concreta de la masa por la distancia que la separa al eje de giro.
- Momento de fuerza (M): o par motor es la fuerza aplicada por la distancia al eje de giro (es el equivalente a la fuerza agente del movimiento que cambia el estado de un movimiento rectilíneo).
Paralelismo entre el movimiento rectilíneo y el movimiento circular
A pesar de las diferencias evidentes en su trayectoria, hay
ciertas similitudes entre el movimiento rectilíneo y el circular que
deben mencionarse y que resaltan las similitudes y equivalencias de
conceptos y un paralelismo en las magnitudes utilizadas para
describirlos. Dado un eje de giro y la posición de una partícula puntual
en movimiento circular o giratorio, para una variación de tiempo Δt o un instante dt, dado, se tiene:
Arco descrito o desplazamiento angular
Arco angular o desplazamiento angular es el arco de la circunferencia recorrido por la masa puntual en su trayectoria circular, medido en radianes y representado con las letras griegas (phi) o (theta). Este arco es el desplazamiento efectuado en el movimiento circular y se obtiene mediante la posición angular ( ó ) en la que se encuentra en un momento determinado el móvil y al que se le asocia un ángulo determinado en radianes. Así el arco angular o desplazamiento angular se determinará por la variación de la posición angular entre dos momentos final e inicial concretos (dos posiciones distintas):
Siendo ó el arco angular o desplazamiento angular dado en radianes.
Si se le llama e al espacio recorrido a lo largo de la trayectoria curvilínea de la circunferencia de radio R se tiene que es el producto del radio de la trayectoria circular por la variación de la posición angular (desplazamiento angular):
En ocasiones se denomina al espacio recorrido (del inglés "space"). Nótese que al multiplicar el radio por el ángulo
en radianes, al ser estos últimos adimensionales (arco entre radio), el
resultado es el espacio recorrido en unidades de longitud elegidas para
expresar el radio.
Velocidad angular y velocidad tangencial
- Velocidad angular es la variación del arco angular o posición angular respecto al tiempo. Es representada con la letra (omega minúscula) y viene definida como:
Siendo la segunda ecuación la de la velocidad angular instantánea (derivada de la posición angular con respecto del tiempo).
- Velocidad tangencial de la partícula es la velocidad del objeto en un instante de tiempo (magnitud vectorial con módulo, dirección y sentido determinados en ese instante estudiado). Puede calcularse a partir de la velocidad angular. Si vt es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
Aceleración angular y tangencial
La aceleración angular es la variación de la velocidad angular por unidad de tiempo y se representa con la letra: y se la calcula:
Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
Período y frecuencia
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:
La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en hercios o s-1
Aceleración centrípeta
La aceleración centrípeta, también llamada normal o radial, afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. Se define como:
El término rω2 presente en la componente radial de la aceleración ar. Dado que v = ωr, la aceleración centrípeta también se puede escribir como:
El término 2(dr/dt)ω localizado en la componente tangencial de la aceleración es conocido como la aceleración de Coriolis.
En el movimiento circunferencial, mientras la dirección del vector velocidad va variando punto a punto, la aceleración centrípeta se manifiesta como un vector con origen en el vector posición y con dirección hacia el centro de la circunferencia.
El término rω2 presente en la componente radial de la aceleración ar. Dado que v = ωr, la aceleración centrípeta también se puede escribir como:
El término 2(dr/dt)ω localizado en la componente tangencial de la aceleración es conocido como la aceleración de Coriolis.
En el movimiento circunferencial, mientras la dirección del vector velocidad va variando punto a punto, la aceleración centrípeta se manifiesta como un vector con origen en el vector posición y con dirección hacia el centro de la circunferencia.
Leyes de Newton
Las leyes de Newton, también conocidas como leyes del movimiento de Newton,1 son tres principios a partir de los cuales se explican una gran parte de los problemas planteados en mecánica clásica, en particular aquellos relativos al movimiento de los cuerpos.
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo solo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.12
Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuya resultante no sea nula. Newton toma en consideración, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como tal a la fricción.
En consecuencia, un cuerpo que se desplaza con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
El enunciado fundamental que podemos extraer de la ley de Newton es que
Esta expresión es una ecuación vectorial, ya que las fuerzas llevan dirección y sentido. Por otra parte, cabe destacar que la variación con la que varía la velocidad corresponde a la aceleración.
Un sistema de referencia con aceleración (y la aceleración normal de un sistema rotatorio se incluye en esta definición) no es un sistema inercial, y la observación de una partícula en reposo en el propio sistema no satisfará las leyes de Newton (puesto que se observará aceleración sin la presencia de fuerza neta alguna). Se denominan sistemas de referencia no inerciales.
Tras la rotura, la fuerza neta ejercida sobre la bola es 0, por lo que experimentará, como resultado de un estado de reposo, un movimiento rectilíneo uniforme.
Primera ley de Newton o ley de inercia
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo solo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.12
Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuya resultante no sea nula. Newton toma en consideración, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como tal a la fricción.
En consecuencia, un cuerpo que se desplaza con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.
El enunciado fundamental que podemos extraer de la ley de Newton es que
Esta expresión es una ecuación vectorial, ya que las fuerzas llevan dirección y sentido. Por otra parte, cabe destacar que la variación con la que varía la velocidad corresponde a la aceleración.
Sistemas de referencia inerciales
La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como sistemas de referencia inerciales, que son aquellos desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.Un sistema de referencia con aceleración (y la aceleración normal de un sistema rotatorio se incluye en esta definición) no es un sistema inercial, y la observación de una partícula en reposo en el propio sistema no satisfará las leyes de Newton (puesto que se observará aceleración sin la presencia de fuerza neta alguna). Se denominan sistemas de referencia no inerciales.
- Observador inercial: desde su punto de vista el bloque se mueve en círculo con velocidad v y está acelerado hacia el centro de la plataforma con una aceleración centrípeta . Esta aceleración es consecuencia de la fuerza ejercida por la tensión de la cuerda.
- Observador no inercial: para el observador que gira con la plataforma el objeto está en reposo, a = 0. Es decir, observa una fuerza ficticia que contrarresta la tensión para que no haya aceleración centrípeta. Esa fuerza debe ser . Este observador siente la fuerza como si fuera perfectamente real, aunque solo sea la consecuencia de la aceleración del sistema de referencia en que se encuentra.
Aplicación de la primera ley de Newton
Se puede considerar como ejemplo ilustrativo de esta primera ley una bola atada a una cuerda, de modo que la bola gira siguiendo una trayectoria circular. Debido a la fuerza centrípeta de la cuerda (tensión), la masa sigue la trayectoria circular, pero si en algún momento la cuerda se rompiese, la bola tomaría una trayectoria rectilínea en la dirección de la velocidad que tenía la bola en el instante de rotura.Tras la rotura, la fuerza neta ejercida sobre la bola es 0, por lo que experimentará, como resultado de un estado de reposo, un movimiento rectilíneo uniforme.
Segunda ley de Newton o ley fundamental de la dinámica
La Segunda Ley de Newton expresa que:
El cambio de movimiento es directamente proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.13
Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.14
Si la masa es constante
Si la masa del cuerpo es constante se puede establecer la siguiente relación, que constituye la ecuación fundamental de la dinámica:Fresultante = maDonde m es la masa del cuerpo la cual debe ser constante para ser expresada de tal forma. La fuerza neta que actúa sobre un cuerpo, también llamada fuerza resultante, es el vector suma de todas las fuerzas que sobre él actúan. Así pues:15
- La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.
- Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.
- Esta es una ecuación vectorial, luego se debe cumplir componente a componente.
- En ocasiones será útil recordar el concepto de componentes intrínsecas: si la trayectoria no es rectilínea es porque hay una aceleración normal, luego habrá también una fuerza normal (en dirección perpendicular a la trayectoria); si el módulo de la velocidad varía es porque hay una aceleración en la dirección de la velocidad (en la misma dirección de la trayectoria).
- La fuerza y la aceleración son vectores paralelos, pero esto no significa que el vector velocidad sea paralelo a la fuerza. Es decir, la trayectoria no tiene por qué ser tangente a la fuerza aplicada (sólo ocurre si al menos, la dirección de la velocidad es constante).
- Esta ecuación debe cumplirse para todos los cuerpos. Cuando analicemos un problema con varios cuerpos y diferentes fuerzas aplicadas sobre ellos, deberemos entonces tener en cuenta las fuerzas que actúan sobre cada uno de ellos y el principio de superposición de fuerzas. Aplicaremos la segunda ley de Newton para cada uno de ellos, teniendo en cuenta las interacciones mutuas y obteniendo la fuerza resultante sobre cada uno de ellos.
 Representación del sumatorio de las fuerzas. Aquí se está sumando dos veces la fuerza No. 2. La resultante (marcada con rojo) responde a la siguiente ecuación:
Representación del sumatorio de las fuerzas. Aquí se está sumando dos veces la fuerza No. 2. La resultante (marcada con rojo) responde a la siguiente ecuación:

El principio de superposición establece que si varias fuerzas actúan igual o simultáneamente sobre un cuerpo, la fuerza resultante es igual a la suma vectorial de las fuerzas que actúan independientemente sobre el cuerpo (regla del paralelogramo). Este principio aparece incluido en los Principia de Newton como Corolario 1, después de la tercera ley, pero es requisito indispensable para la comprensión y aplicación de las leyes, así como para la caracterización vectorial de las fuerzas.14 La fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. Las fuerzas son causas que producen aceleraciones en los cuerpos. Por lo tanto existe una relación causa-efecto entre la fuerza aplicada y la aceleración que se este cuerpo experimenta.
De esta ecuación se obtiene la unidad de medida de la fuerza en el Sistema Internacional de Unidades, el Newton:
Por otra parte, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de esta (debido a que la masa siempre es un escalar positivo). La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista.
Si la masa no es constante
Si la masa de los cuerpos varía, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = ma y hay que hacer genérica la ley para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero hay que definir una magnitud física nueva, la cantidad de movimiento, que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:p = mvNewton enunció su ley de una forma más general:
De esta forma se puede relacionar la fuerza con la aceleración y con la masa, sin importar que esta sea o no sea constante. Cuando la masa es constante sale de la derivada con lo que queda la expresión:
Y se obtiene la expresión clásica de la Segunda Ley de Newton:
La fuerza, por lo tanto, es un concepto matemático el cual, por definición, es igual a la derivada con respecto al tiempo del momento de una partícula dada, cuyo valor a su vez depende de su interacción con otras partículas. Por consiguiente, se puede considerar la fuerza como la expresión de una interacción. Otra consecuencia de expresar la Segunda Ley de Newton usando la cantidad de movimiento es lo que se conoce como principio de conservación de la cantidad de movimiento: si la fuerza total que actúa sobre un cuerpo es cero, la Segunda ley de Newton nos dice que
Es decir, la derivada de la cantidad de movimiento con respecto al tiempo es cero en sus tres componentes. Esto significa que la cantidad de movimiento debe ser constante en el tiempo en módulo dirección y sentido (la derivada de un vector constante es cero).16
La segunda ley de Newton solo es válida en sistemas de referencia inerciales pero incluso si el sistema de referencia es no inercial, se puede utilizar la misma ecuación incluyendo las fuerzas ficticias (o fuerzas inerciales). Unidades y dimensiones de la fuerza:
- Unidades S.I.:
- Sistema cegesimal: dina
- Equivalencia: 1 N= 10⁵ dinas
Cantidad de movimiento o momento lineal
En el lenguaje moderno la cantidad de movimiento o momento lineal de un objeto se define mediante la expresión p = mv. Es decir, es una magnitud vectorial proporcional a la masa y a la velocidad del objeto. Partiendo de esta definición y aplicando la ley fundamental de la mecánica de Newton, las variaciones de la cantidad de movimiento se expresan en función de la fuerza resultante y el intervalo de tiempo durante el cual se ejerce esta:Tomando el intervalo de tiempo de t1 a t2 e integrando se obtiene
Al vector I se le denomina impulso lineal y representa una magnitud física que se manifiesta especialmente en las acciones rápidas o impactos, tales como choques, llevando módulo dirección y sentido. En este tipo de acciones conviene considerar la duración del impacto y la fuerza ejercida durante el mismo.
De la expresión obtenida se deduce que el impulso lineal es igual a la variación de la cantidad de movimiento. Si la fuerza resultante es cero (es decir, si no se actúa sobre el objeto) el impulso también es cero y la cantidad de movimiento permanece constante. Llamamos a esta afirmación ley de conservación del impulso lineal, aplicada a un objeto o una partícula.17
Sus unidades en el Sistema Internacional son
- Conservación de la cantidad de movimiento
Bolas representando choque elástico
- Choque elástico: permanecen constantes la cantidad de movimiento y la energía cinética. Dos partículas de masas diferentes que solo interactúan entre sí y que se mueven con velocidades constantes y distintas una hacia la otra. Tras el choque, permanece constante la cantidad de movimiento y la energía cinética.
Coches representando choque inelástico
- Choque inelástico: permanece constante la cantidad de movimiento y varía la energía cinética. Como consecuencia, los cuerpos que colisionan pueden sufrir deformaciones y aumento de su temperatura. Tras un choque totalmente inelástico, ambos cuerpos tienen la misma velocidad. La suma de sus energías cinéticas es menor que la inicial porque una parte de esta se ha transformado en energía interna; en la mayoría de los casos llega a ser disipada en forma de calor debido al calentamiento producido en el choque. En el caso ideal de un choque perfectamente inelástico entre objetos macroscópicos, estos permanecen unidos entre sí tras la colisión.18
Aplicaciones de la segunda ley de Newton
Entre las posibles aplicaciones de la Segunda Ley de Newton, se pueden destacar:- Caída libre: es un movimiento que se observa cuando un objeto se deja caer desde una cierta altura sobre la superficie de la tierra. Para estudiar el movimiento se elige un sistema de coordenadas donde el origen del eje y está sobre esta última. En este sistema tanto la velocidad de caída como la aceleración de la gravedad tienen signo negativo. En el ejemplo representado, se supone que el objeto se deja caer desde el reposo, pero es posible que caiga desde una velocidad inicial distinta de cero.18
Péndulo Simple: Diagrama de Fuerzas
- Péndulo simple: partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable. Si la partícula se desplaza a una posición θ0 (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar. El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Las fuerzas que actúan sobre la partícula de masa m son dos, el peso y la tensión T del hilo.
donde an representa la aceleración normal a la trayectoria. Conocido el valor de la velocidad v en la posición angular se puede determinar la tensión T del hilo. Esta es máxima cuando el péndulo pasa por la posición de equilibrio
,donde el segundo término representa la fuerza centrífuga.
Y la tensión es mínima, en los extremos de su trayectoria, cuando la velocidad es cero
en la dirección tangencial:
donde at representa la aceleración tangente a la trayectoria.
Tercera ley de Newton o principio de acción y reacción
La tercera ley de Newton establece que siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección pero en sentido opuesto sobre el primero. Con frecuencia se enuncia así: A cada acción siempre se opone una reacción igual pero de sentido contrario. En cualquier interacción hay un par de fuerzas de acción y reacción situadas en la misma dirección con igual magnitud y sentidos opuestos. La formulación original de Newton es:
Con toda acción ocurre siempre una reacción igual y contraria: quiere decir que las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.13
Esta tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otra manera por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.19 Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto. Si dos objetos interaccionan, la fuerza F12, ejercida por el objeto 1 sobre el objeto 2, es igual en magnitud con misma dirección pero sentidos opuestos a la fuerza F21 ejercida por el objeto 2 sobre el objeto 1:20
La fuerza de reacción (flecha verde) aumenta conforme aumenta la aplicada al objeto, la fuerza aplicada (flecha roja)
Aplicaciones de la Tercera Ley de Newton
Algunos ejemplos donde actúan las fuerzas acción-reacción son los siguientes:20- Si una persona empuja a otra de peso similar, las dos se mueven con la misma velocidad pero en sentido contrario.
- Cuando saltamos, empujamos a la tierra hacia abajo, que no se mueve debido a su gran masa, y esta nos empuja con la misma intensidad hacia arriba.
- Una persona que rema en un bote empuja el agua con el remo en un sentido y el agua responde empujando el bote en sentido opuesto.
- Cuando caminamos empujamos a la tierra hacia atrás con nuestros pies, a lo que la tierra responde empujándonos a nosotros hacia delante, haciendo que avancemos.
- Cuando se dispara una bala, la explosión de la pólvora ejerce una fuerza sobre la pistola (que es el retroceso que sufren las armas de fuego al ser disparadas), la cual reacciona ejerciendo una fuerza de igual intensidad pero en sentido contrario sobre la bala.
- La fuerza de reacción que una superficie ejerce sobre un objeto apoyado en ella, llamada fuerza normal con dirección perpendicular a la superficie.
- Las fuerzas a distancia no son una excepción, como la fuerza que la Tierra ejerce sobre la Luna y viceversa, su correspondiente pareja de acción y reacción:21
.
Además, la fuerza que la Luna ejerce sobre la Tierra es también responsable de las mareas, pues conforme la Luna gira alrededor de la Tierra esta ejerce una fuerza de atracción sobre la superficie terrestre, la cual eleva los mares y océanos, elevando varios metros el nivel del agua en algunos lugares; por este motivo esta fuerza también se llama fuerza de marea. La fuerza de marea de la luna se compone con la fuerza de marea del sol proporcionando el fenómeno completo de las mareas.
Ley de elasticidad de Hooke
La ley de Hooke: la fuerza es proporcional a la extensión
siendo el alargamiento, L la longitud original, E: módulo de Young, A la sección transversal de la pieza estirada. La ley se aplica a materiales elásticos hasta un límite denominado límite elástico.
Esta ley recibe su nombre de Robert Hooke, físico británico contemporáneo de Isaac Newton, y contribuyente prolífico de la arquitectura. Esta ley comprende numerosas disciplinas, siendo utilizada en ingeniería y construcción, así como en la ciencia de los materiales. Ante el temor de que alguien se apoderara de su descubrimiento, Hooke lo publicó en forma de un famoso anagrama, ceiiinosssttuv, revelando su contenido un par de años más tarde. El anagrama significa Ut tensio sic vis ("como la extensión, así la fuerza").
Ley de Hooke para los resortes
La ley de Hooke describe cuánto se alargará un resorte bajo una cierta fuerza.
donde k se llama constante elástica del resorte y es su elongación o variación que experimenta su longitud.
La energía de deformación o energía potencial elástica Uk asociada al estiramiento del resorte viene dada por la siguiente ecuación:
Es importante notar que la k antes definida depende de la longitud del muelle y de su constitución. Definiremos ahora una constante intrínseca del resorte independiente de la longitud de este y estableceremos así la ley diferencial constitutiva de un muelle. Multiplicando k por la longitud total, y llamando al producto ki o k intrínseca, se tiene:
Llamaremos a la tensión en una sección del muelle situada una distancia x de uno de sus extremos el cual tomaremos como origen de coordenadas, a la constante de un pequeño trozo de muelle de longitud a la misma distancia y al alargamiento de ese pequeño trozo en virtud de la aplicación de la fuerza . Por la ley del muelle completo:
Tomando el límite:
que por el principio de superposición resulta:
Que es la ecuación diferencial del muelle. Si se integra para todo x, se obtiene como ecuación de onda unidimensional que describe los fenómenos ondulatorios (Ver: Muelle elástico). La velocidad de propagación de las vibraciones en un resorte se calcula como:
Máquina de Atwood
La máquina de Atwood es una máquina inventada en 1784 por George Atwood
como un experimento de laboratorio para verificar las leyes mecánicas
del movimiento uniformemente acelerado. La máquina de Atwood es una
demostración común en las aulas usada para ilustrar los principios de la
Física, específicamente en Mecánica.
La máquina de Atwood consiste en dos masas, m1 y m2, conectadas por una cuerda inelástica de masa despreciable con una polea ideal de masa despreciable.
La máquina de Atwood consiste en dos masas, m1 y m2, conectadas por una cuerda inelástica de masa despreciable con una polea ideal de masa despreciable.
- Cuando m1 = m2,, la máquina está en equilibrio neutral sin importar la posición de los pesos.
- Cuando m2 > m3, ambas masas experimentan una aceleración uniforme
Ecuación para la aceleración uniforme
Se puede obtener una ecuación para la aceleración usando análisis de fuerzas. Puesto que se está usando una cuerda inelástica con masa despreciable y una polea ideal con masa despreciable, las únicas fuerzas que se tiene que considerar son: la fuerza tensión (T) y el peso de las dos masas (mg). Para encontrar el tenemos que considerar las fuerzas que afectan a cada masa por separado (con el siguiente convenio de signos, suponiendo que m1 > m2, la aceleración a es positiva hacia "abajo" -con el mismo sentido de la aceleración de la gravedad g- en m1 y hacia "arriba" -con el sentido contrario a la aceleración de la gravedad g- en m2):
- fuerzas que afectan a m1 : m1 g - T = m2 a(donde g y a tienen el mismo sentido)
- fuerzas que afectan a m2 : T - m2 g = m2 a(donde T y a tienen el mismo sentido)
Usando la segunda Ley de Newton del movimiento se puede obtener una ecuación para la aceleración del sistema de Atwood .
El factor , con m1 > m2,
es el número adimensional denominado número de Atwood en honor de George Atwood.
[Nota: Inversamente, la aceleración debida a la gravedad (g) puede obtenerse cronometrando el movimiento de los pesos y calculando un valor para la aceleración uniforme (a): En el diagrama de la figura, si se parte de las masas alineadas y se mide el tiempo t12 en el que se separan las masas una distancia vertical d12, se cumple que
. Entonces: ]
Ecuación para la tensión
Puede ser útil obtener una ecuación para la tensión en la cuerda. Para evaluar la tensión sustituimos la ecuación por la aceleración en cualquiera de las dos ecuaciones de fuerza.
Por ejemplo sustituyendo en m2 a = T - m2 g, se obtiene:
La tensión puede obtenerse de una forma similar de m1 a = m1 g - T
Ecuación para una polea no lineal
Para diferencias muy pequeñas de masa y entre m1 > m2, el momento de inercia (I) sobre la polea de masa no despreciable de radio r no puede ser despreciada. La aceleración angular de la polea viene dada por:
En este caso, el torque total del sistema se convierte en:
Implementaciones prácticas
Las ilustraciones originales de Atwood muestran el eje de la polea principal descansando sobre el borde de otras cuatro ruedas, para minimizar las fuerzas de fricción de los cojinetes. Muchas implementaciones históricas de la máquina siguen este diseño.Un ascensor con un contrapeso se aproxima a una máquina de Atwood ideal y de ese modo alivia al motor conductor de la carga total de la cabina del ascensor —solo tiene que vencer la diferencia entre el peso y la inercia de las dos masas, contrapeso y cabina-. El mismo principio se usa para ferrocarriles funiculares con dos vagones conectados en vías inclinadas.
Fricción
La fuerza de fricción o la fuerza de rozamiento es la fuerza que existe entre dos superficies en contacto, que se opone al movimiento relativo entre ambas superficies (fuerza de fricción dinámica) o a la fuerza que se opone al inicio del deslizamiento (fuerza de fricción estática). Se genera debido a las imperfecciones, mayormente microscópicas, entre las superficies en contacto. Estas imperfecciones hacen que la fuerza perpendicular R entre ambas superficies no lo sea perfectamente, sino que forme un ángulo con la normal N (el ángulo de rozamiento). Por tanto, la fuerza resultante se compone de la fuerza normal N (perpendicular a las superficies en contacto) y de la fuerza de rozamiento F, paralela a las superficies en contacto.
Rozamiento entre superficies de dos sólidos
En el rozamiento entre dos cuerpos se ha observado los siguientes hechos:
- La fuerza de rozamiento tiene dirección paralela a la superficie de apoyo.
- El coeficiente de rozamiento depende exclusivamente de la naturaleza de los cuerpos en contacto, así como del estado en que se encuentren sus superficies.
- La fuerza máxima de rozamiento es directamente proporcional a la fuerza normal que actúa entre las superficies de contacto.
- Para un mismo par de cuerpos (superficies de contacto), el rozamiento es mayor un instante antes de que comience el movimiento que cuando ya ha comenzado (estático Vs. cinético).
El rozamiento puede variar en una medida mucho menor debido a otros factores:
- El coeficiente de rozamiento es prácticamente independiente del área de las superficies de contacto.
- El coeficiente de rozamiento cinético es prácticamente independiente de la velocidad relativa entre los móviles.
- La fuerza de rozamiento puede aumentar ligeramente si los cuerpos llevan mucho tiempo sin moverse uno respecto del otro ya que pueden sufrir atascamientoentre sí.
Algunos autores sintetizan las leyes del comportamiento de la fricción en los siguientes dos postulados básicos:1
- La resistencia al deslizamiento tangencial entre dos cuerpos es proporcional a la fuerza normal ejercida entre los mismos.
- La resistencia al deslizamiento tangencial entre dos cuerpos es independiente de las dimensiones de contacto entre ambos.
La segunda ley puede ilustrarse arrastrando un bloque sobre una superficie plana. La fuerza de arrastre será la misma aunque el bloque descanse sobre la cara ancha o sobre un borde más angosto. Estas leyes fueron establecidas primeramente por Leonardo da Vinci al final del siglo XV, olvidándose después durante largo tiempo; posteriormente fueron redescubiertas por el ingeniero francés Amontons en 1699. Frecuentemente se les denomina también leyes de Amontons.
Tipos de fricción
Existen dos tipos de rozamiento o fricción, la fricción estática (Fe) y la fricción dinámica (Fd). El primero es la resistencia que se debe superar para poner en movimiento un cuerpo con respecto a otro que se encuentra en contacto. El segundo, es la resistencia, de magnitud considerada constante, que se opone al movimiento pero una vez que este ya comenzó. En resumen, lo que diferencia a un roce con el otro, es que el estático actúa cuando los cuerpos están en reposo relativo en tanto que el dinámico lo hace cuando ya están en movimiento.
La fuerza de fricción estática, necesaria para vencer la fricción homóloga, es siempre menor o igual al coeficiente de rozamiento entre los dos objetos (número medido empíricamente y que se encuentra tabulado) multiplicado por la fuerza normal. La fuerza cinética, en cambio, es igual al coeficiente de rozamiento dinámico, denotado por la letra griega , por la normal en todo instante.
No se tiene una idea perfectamente clara de la diferencia entre el rozamiento dinámico y el estático, pero se tiende a pensar que el estático es algo mayor que el dinámico, porque al permanecer en reposo ambas superficies pueden aparecer enlaces iónicos, o incluso microsoldaduras entre las superficies, factores que desaparecen en estado de movimiento. Este fenómeno es tanto mayor cuanto más perfectas son las superficies. Un caso más o menos común es el del gripaje de un motor por estar mucho tiempo parado (no solo se arruina por una temperatura muy elevada), ya que al permanecer las superficies, del pistón y la camisa, durante largo tiempo en contacto y en reposo, pueden llegar a soldarse entre sí.
Un ejemplo bastante común de fricción dinámica es la ocurrida entre los neumáticos de un auto y el pavimento en un frenado abrupto.
Como comprobación de lo anterior, se realiza el siguiente ensayo, sobre una superficie horizontal se coloca un cuerpo, y le aplica una fuerza horizontal F , muy pequeña en un principio, se puede ver que el cuerpo no se desplaza, la fuerza de rozamiento iguala a la fuerza aplicada y el cuerpo permanece en reposo, en la gráfica se representa en el eje horizontal la fuerza F aplicada, y en el eje vertical la fuerza de rozamiento Fr.
Entre los puntos O y A, ambas fuerzas son iguales y el cuerpo permanece estático; al sobrepasar el punto A el cuerpo súbitamente se comienza a desplazar, la fuerza ejercida en A es la máxima que el cuerpo puede soportar sin deslizarse, se denomina Fe o fuerza estática de fricción; la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado el desplazamiento es Fd o fuerza dinámica, es menor que la que fue necesaria para iniciarlo (Fe). La fuerza dinámica permanece constante.
Si la fuerza de rozamiento Fr es proporcional a la normal N, y a la constante de proporcionalidad se la llama :
Y permaneciendo la fuerza normal constante, se puede calcular dos coeficientes de rozamiento: el estático y el dinámico como:
donde el coeficiente de rozamiento estático corresponde al de la mayor fuerza que el cuerpo puede soportar inmediatamente antes de iniciar el movimiento y el coeficiente de rozamiento dinámico corresponde a la fuerza necesaria para mantener el cuerpo en movimiento una vez iniciado.
Fricción estática
Es la fuerza que se opone al inicio del deslizamiento. Sobre un cuerpo en reposo al que se aplica una fuerza horizontal F, intervienen cuatro fuerzas:
- F: la fuerza aplicada.
- Fr: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.
- P: el peso del propio cuerpo
- N: la fuerza normal.
Dado que el cuerpo está en reposo la fuerza aplicada y la fuerza de rozamiento son iguales, y el peso del cuerpo y la normal:
Se sabe que el peso del cuerpo P es el producto de su masa por la aceleración de la gravedad (g), y que la fuerza de rozamiento es el coeficiente estático por la normal:
esto es:
La fuerza horizontal F máxima que se puede aplicar a un cuerpo en reposo es igual al coeficiente de rozamiento estático por su masa y por la aceleración de la gravedad.
Fricción dinámica
Dado un cuerpo en movimiento sobre una superficie horizontal, deben considerarse las siguientes fuerzas:
- Fa: la fuerza aplicada.
- Fr: la fuerza de rozamiento entre la superficie de apoyo y el cuerpo, y que se opone al deslizamiento.
- P: el peso del propio cuerpo, igual a su masa por la aceleración de la gravedad.
- N: la fuerza normal, que la superficie hace sobre el cuerpo sosteniéndolo.
Como equilibrio dinámico, se puede establecer que:
Sabiendo que:
prescindiendo de los signos para tener en cuenta solo las magnitudes, se puede reescribir la segunda ecuación de equilibrio dinámico como:
Es decir, la fuerza de empuje aplicada sobre el cuerpo es igual a la fuerza resultante menos la fuerza de rozamiento que el cuerpo opone a ser acelerado. De esa esa misma expresión se deduce que la aceleración que sufre el cuerpo, al aplicarle una fuerza Fa mayor que la fuerza de rozamiento Fr con la superficie sobre la que se apoya.
Rozamiento en un plano inclinado
Rozamiento estático
Si sobre una línea horizontal r, se tiene un plano inclinado un ángulo , y sobre este plano inclinado se coloca un cuerpo con rozamiento, se tendrán tres fuerzas que intervienen:
- P: el peso del cuerpo vertical hacia abajo según la recta u, y con un valor igual a su masa por la aceleración de la gravedad: P = mg.
- N: la fuerza normal que hace el plano sobre el cuerpo, perpendicular al plano inclinado, según la recta t
- Fr: la fuerza de rozamiento entre el plano y el cuerpo, paralela al plano inclinado y que se opone a su deslizamiento.
Si el cuerpo está en equilibrio, no se desliza, la suma vectorial de estas tres fuerzas es cero:
Lo que gráficamente seria un triángulo cerrado formado por estas tres fuerzas, puestas una a continuación de otra, como se ve en la figura.
El peso puede descomponerse en una componente normal al plano Pn y una componentes tangente al plano Pt y la ecuación anterior puede escribirse componente a componentes simplemente como:
Dividiendo la primera componente entre la segunda se obtiene como resultado:
El coeficiente de rozamiento estático es igual a la tangente del ángulo del plano inclinado, en el que el cuerpo se mantiene en equilibrio sin deslizar, ello permite calcular los distintos coeficientes de rozamiento, simplemente colocando un cuerpo de un material concreto sobre un plano inclinado del material con el que se pretende calcular su coeficiente de rozamiento, inclinando el plano progresivamente se observa el momento en el que el cuerpo comienza a deslizarse, la tangente de este ángulo es el valor del coeficiente de rozamiento. Del mismo modo conocido el coeficiente de rozamiento entre dos materiales podemos saber el ángulo máximo de inclinación que puede soportar sin deslizar.
Rozamiento dinámico
En el caso de rozamiento dinámico en un plano inclinado, se tiene un cuerpo que se desliza, y siendo que está en movimiento, el coeficiente que interviene es el dinámico , así como una fuerza de inercia Fi, que se opone al movimiento, el equilibrio de fuerzas se da cuando:
descomponiendo los vectores en sus componentes normales y tangenciales se tiene:
teniendo en cuenta que:
y como en el caso de equilibrio estático, se tiene:
Con estas ecuaciones se determina las condiciones de equilibrio dinámico del cuerpo con fricción en un plano inclinado. Si el cuerpo se desliza sin aceleración (a velocidad constante) su fuerza de inercia Fi será cero, y se puede ver que:
esto es, de forma semejante al caso estático:
con lo que se puede decir que el coeficiente de rozamiento dinámico de un cuerpo con la superficie de un plano inclinado, es igual a la tangente del ángulo del plano inclinado con el que el cuerpo se desliza sin aceleración, con velocidad constante, por el plano.
Valores de los coeficientes de fricción
| Materiales en contacto | ||
|---|---|---|
| Articulaciones humanas | 0,02 | 0,003 |
| Acero // Hielo | 0,028 | 0,09 |
| Acero // Teflón | 0,04 | 0,04 |
| Teflón // Teflón | 0,04 | 0,04 |
| Hielo // Hielo | 0,1 | 0,03 |
| Esquí (encerado) // Nieve (0 °C) | 0,1 | 0,05 |
| Acero // Acero | 0,15 | 0,09 |
| Vidrio // Madera | 0,25 | 0,2 |
| Caucho // Cemento (húmedo) | 0,3 | 0,25 |
| Madera // Cuero | 0,5 | 0,4 |
| Caucho // Madera | 0,7 | 0,6 |
| Acero // Latón | 0,5 | 0,4 |
| Madera // Madera | 0,7 | 0,4 |
| Madera // Piedra | 0,7 | 0,3 |
| Vidrio // Vidrio | 0,9 | 0,4 |
| Caucho // Cemento (seco) | 1 | 0,8 |
| Cobre // Hierro (fundido) | 1 | 0,3 |
En la tabla se listan los coeficientes de rozamiento de algunas sustancias donde
- Coeficiente de rozamiento estático,
- Coeficiente de rozamiento dinámico.
Los coeficientes de rozamiento, por ser relaciones entre dos fuerzas son magnitudes adimensionales.
UNIDAD V Trabajo y Energía
Trabajo
En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo1 de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra W (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
Ya que por definición el trabajo es un tránsito de energía,2 nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.
| Trabajo (W) | ||
|---|---|---|
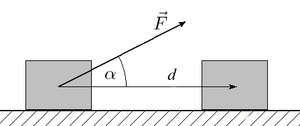 Trabajo realizado por una fuerza constante. |
||
| Magnitud | Trabajo (W) | |
| Definición | Producto de la fuerza ejercida sobre un cuerpo por su desplazamiento | |
| Tipo | Magnitud escalar | |
| Unidad SI | Julio (J) | |
| Otras unidades | Kilojulio (kJ) Kilográmetro (kgm) | |
Trabajo con una fuerza constante
W = F |∆x|
que es el área de la curva en una gráfica Fx vs x
W = Fx∆x = Fcosθ|∆x|
Trabajo total
Se define como la suma de las fuerzas que actúan en el objeto por el desplazamiento del mismo Wtotal = F1x ∆x + F2x ∆x + F3x ∆x + ....
= (F1x + F2x + F3x + ...) ∆x
= Fneta∆x
Energía cinética
Existe una importante relación entre el trabajo neto realizado sobre una partícula y la velocidad de ésta en las posiciones inicial y final. si Fneta es la fuerza neta que actúa sobre una partícula tenemos, según la segunda ley de Newton:
Fneta x = max
Si la fuerza es constante, la aceleración es constante y el desplazamiento está relacionado con la velocidad inicial Vi y con la velocidad final Vf usamos la fórmula
v² = v0² + 2aΔx
válida cuando la velocidad es constante, resolviendo para ax
ax = ½∆x (vf²-vi²)
Sustituyendo ax en Fneta x = max y multiplicando ambos miembros por Δx se tiene
Reconocemos que el primer miembro es el trabajo realizado sobre la partícula. Así
La magnitud ½mv² recibe el nombre de energía cinética Ec de la partícula:
Así el trabajo total realizado sobre la partícula es igual a la variación de energía cinética de la misma (llamado Teorema trabajo - energía cinética).
Trabajo con una fuerza variable
Cuando la fuerza no es constante el trabajo se calcula como la integral de la fuerza por el desplazamiento:
x2
W = ∫ Fx∙dx
x1
El producto escalar de dos vectores en un espacio euclídeo se define como el producto de sus módulos por el coseno del ángulo que forman.
Esta definición de carácter geométrico es independiente del sistema de coordenadas elegido y por lo tanto de la base del espacio vectorial escogida.
Cuando dos vectores forman un ángulo cero, el valor del coseno es la unidad, por lo tanto el producto de los módulos vale lo mismo que el producto escalar.
Propiedades del producto escalar
Sean A, B y C vectores en el plano o en el espacio y sea m un escalar:
1. Conmutativa:
Expresión analítica del producto escalar
Si los vectores A y B se expresan en función de sus componentes cartesianas rectangulares, tomando la base canónica en formada por los vectores unitarios i , j , k tenemos:
Norma o Módulo de un vector
Se define como la longitud del segmento orientado (vector) en el espacio métrico considerado.
Se calcula a través del producto interno del vector consigo mismo.
La componente de un vector a lo largo de un eje puede escribirse como el producto escalar del vector por el vector unitario sobre dicho eje. Por ejemplo la componente Ax se obtiene del producto:
Esta relación sugiere un procedimiento algebraico para obtener una ecuación paras las componentes a partir de una ecuación vectorial. Multiplicando la ecuación vectorial A + B = C por i se obtiene A • i + B • i = C • i que conduce a Ax + Bx = Cx
Derivada del producto punto
Para establecer la regla de la diferenciación del producto escalar, diferenciamos ambos miembros de la ecuación:
A • B = AxBx + AyBy
d (A • B) =d (AxBx + AyBy) = dAx Bx + Ax dBx + dAy By+ Ay dBy
dt dt dt dt dt dt
reordenando y operando:
d (A • B) = dA • B + A • dB
dt dt dt
Diferenciación de un producto escalar por sí mismo, sea v el vector velocidad de modulo v y a es la aceleración.
d(v²) = d (v • v) = dv • v+ v • dv = 2 dv • v
dt dt dt dt dt
por tanto
d (v²) =2a • v
dt
La potencia P suministrada por una fuerza es el trabajo por unidad de tiempo que realiza dicha fuerza. Consideremos una partícula con velocidad instantánea v. En un intervalo corto de tiempo dt, la partícula se desplaza ds = v dt. El trabajo realizado por una fuerza F que actúa sobre la partícula durante ese intervalo de tiempo es:
dW = F • ds = F • v dt
La potencia suministrada por la partícula es
P = dW/dt = F • v
La unidad del SI de potencia, julio por segundo, se denomina (W)
1 W = 1 J /s
Observe la diferencia entre potencia y trabajo. Dos motores que elevan una determinada carga a igual distancia consumen la misma energía, pero el que lo levanta en menos tiempo es más potente.
Potencia y energía cinética
Demostraremos que la potencia transmitida sobre una partícula por la fuerza neta que actúa sobre ella se iguala con la tasa de cambio de la energía cinética de la partícula.
Como la potencia transmitida por la fuerza viene dada por Fneta • v. Demostraremos que Fneta • v = dEc/dt, donde Ec = ½mv²
Como
2a • v = d (v²)
dt
de F = ma tenemos que
2 Fneta • v
m
Fneta • v = m d (v²) = d (½ mv²)
2 dt dt
Pneta = d (½ mv²) = dEc
dt dt
Trabajo y energía en tres dimensiones
De lo anterior podemos establecer el Teorema trabajo - energía cinética en tres dimensiones, y puede establecerse integrando los dos términos de esta ecuación con respecto del tiempo. Esto nos conduce a:
t2 t2
∫Fneta • v dt = ∫(dEc/dt)dt
t1 t1
como ds = v dt, donde ds es el desplzamiento durante el tiempo dt, y teniendo en cuenta, además, que (dEc/dt)dt = dEc la ecuación anterior puede expresarse:
2 2
∫Fneta • ds = ∫dEc
1 1
en donde la integral de la izquierda es el trabajo total Wtotal realizado sobre la partícula. El primer miembro de la expresión anterior puede integrarse, lo cual lleva a
2
Wtotal = ∫Fneta • ds = Ec2 - Ec1 = ∆Ec
1
La energía potencial es la energía mecánica asociada a la localización de un cuerpo dentro de un campo de fuerzas (gravitatoria, electrostática, etc.) o a existencia de un campo de fuerzas en el interior de un cuerpo (energía elástica). La energía potencial de un cuerpo es una consecuencia de la que el sistema de fuerzas que actúa sobre un cuerpo sea conservativo.
Independientemente de la fuerza que la origine, la energía potencial que posee el sistema físico representa la energía "almacenada" en virtud de su posición y/o configuración, por contraposición con la energía cinética que tiene y que representa su energía debida al movimiento. Para un sistema conservativo, la suma de energía cinética y potencial es constante, eso justifica el nombre de fuerzas conservativas, es decir, aquellas que hacen que la energía "se conserve". El concepto de energía potencial también puede usarse para sistemas físicos en los que intervienen fuerzas disipativas, y que por tanto no conservan la energía, sólo que en ese caso la energía mecánica total no será constante, y para aplicar el principio de conservación de la energía es necesario contabilizar la disipación de energía.1
El valor de la energía potencial depende siempre del punto o configuración de referencia escogido para medirla, por esa razón se dice a veces que físicamente sólo importa la variación de energía potencial entre dos configuraciones.2.
La energía potencial interviene como se ha mencionado en el principio de conservación de la energía y su campo de aplicación es muy general. Está presente no solo en la física clásica, sino también de la física relativista y física cuántica. El concepto se ha generalizado también a la física de partículas, donde se han llegado a utilizar potenciales complejos con el objeto de incluir también la energía disipada por el sistema.3
Fuerzas conservativas
Una fuerza es conservativa si el trabajo total que realiza sobre una partícula es cero, cuando la partícula recorre una trayectoria cerrada y vuelve a su posición inicial.
El trabajo realizado por una fuerza conservativa es independiente de la trayectoria seguida por la partícula cuando se mueve de un punto a otro.
Como el trabajo realizado por una fuerza conservativa sobre una partícula no depende de la trayectoria, sólo depende de los puntos 1 y 2. Podemos usar esta propiedad para definir la función energía potencial U, asociada a una fuerza conservativa. En general, la función energía potencial se define de tal modo que el trabajo realizado por una fuerza conservativa sea igual a la disminución de la función energía-potencial:
2
W = ∫F • ds = -∆U
1
es decir,
2
∆U= U2 - U1 = - ∫F • ds
1
Energía potencial de un muelle
Otro ejemplo de una fuerza conservativa es la que ejerce un muelle estirado (o comprimido). Supongamos que tiramos de un bloque atado a un muelle y lo desplazamos de una posición x=0 (equilibrio) a otra x1.
El muelle realiza un trabajo negativo porque su fuerza se opone a la dirección del movimiento. Si ahora dejamos el bloque en libertad, el muelle realiza un trabajo positivo, al acelerar el bloque hacia su posición inicial. el trabajo total realizado por el muelle para mover el bloque hasta su posición inicial x = x1 y devolverlo luego a x=0 es cero, independientemente del valor de x1 (siempre que el alargamiento no supere el límite de elasticidad del muelle). La fuerza que ejerce el muelle es, por lo tanto, una fuerza conservativa.
Calculando la función energía potencial asociada a esta fuerza tenemos:
dU = -F ds = -Fx dx = -(-kx)dx = +kx dx
por lo tanto
U = ∫kx dx = ½ kx² + U0
en donde U0 es la energía potencial para x=0 es decir, cuando el muelle esta sin tensar. Haciendo U0 igual a cero resulta:
U = ½ k x²
Cuando tiramos del bloque desde x=0 hasta x=x1, ejercemos una fuerza aplicada sobre el muelle. Si el bloque inicia su movimiento en x=0 y lo acaba en x=x1, en ambos casos en reposo, el cambio de su energía cinética es cero. El teorema trabajo-energía implica que el trabajo total realizado sobre el bloque es cero, es decir Wap + Wmuelle = 0
Wap = - Wmuelle = ∆Umuelle = ½ kx1² - 0 = ½ kx1²
Este trabajo se almacena en forma de energía potencial en el sistema muelle - bloque.
Fuerzas no conservativas
En contraposición, las fuerzas no conservativas son aquellas en las que el trabajo a lo largo de un camino cerrado es distinto de cero. Estas fuerzas realizan más trabajo cuando el camino es más largo, por lo tanto el trabajo no es independiente del camino.
No todas las fuerza con conservativas. Supongamos que se empuja desde un punto A hasta un punto B una caja situada encima de una mesa y luego se vuelve de B a A, de forma que la caja en el mismo sitio de donde ha salido. El rozamiento se opone al movimiento, por lo que la fuerza que se ejerce al empujar la caja, que siempre va en la dirección del movimiento, realiza un trabajo positivo en los dos tramos del trayecto. Por lo tanto, el trabajo total que ha hecho el empuje no es cero y nos encontramos ante un ejemplo de fuerza no conservativa para la cual no podemos definir una función energía potencial.
Energía potencial y equilibrio
Para una fuerza conservativa general en una dimensión, F = Fxi tenemos
dU = -F • ds = -Fx dx
La fuerza es, por tanto, la derivada negativa de la función energía potencial
Fx = -dU/dx
Esta expresión general puede comprobarse para el caso de un sistema bloque-muelle diferenciando la función U = ½ k x² , con lo que obtenemos
Fx = -dU/dx = d (½ k x² ) = -kx
dx
Una partícula está en equilibrio si la fuerza neta que actúa sobre ella es nula.
Fneta xΔx = ½mv²f - ½mv²i
Reconocemos que el primer miembro es el trabajo realizado sobre la partícula. Así
Wtotal = ½mv²f - ½mv²i
La magnitud ½mv² recibe el nombre de energía cinética Ec de la partícula:
Ec = ½mv²
Así el trabajo total realizado sobre la partícula es igual a la variación de energía cinética de la misma (llamado Teorema trabajo - energía cinética).
Wtotal = ΔEc
Trabajo con una fuerza variable
Cuando la fuerza no es constante el trabajo se calcula como la integral de la fuerza por el desplazamiento:
x2
W = ∫ Fx∙dx
x1
que es el área de la curva en la gráfica Fx vs x
Producto escalar de dos vectores
El producto escalar de dos vectores en un espacio euclídeo se define como el producto de sus módulos por el coseno del ángulo que forman.
En los espacios euclídeos, la notación usual de producto escalar es
Esta definición de carácter geométrico es independiente del sistema de coordenadas elegido y por lo tanto de la base del espacio vectorial escogida.
Proyección de un vector sobre otro
Puesto que |A| cos θ representa el módulo de la proyección del vector A sobre la dirección del vector B, esto es |A| cos θ = proy AB, seráde modo que el producto escalar de dos vectores también puede definirse como el producto del módulo de uno de ellos por la proyección del otro sobre él.
Ángulos entre dos vectores
La expresión geométrica del producto escalar permite calcular el coseno del ángulo existente entre los vectores, mediante la siguiente definición formal: que nos dice que la multiplicación de un escalar denominado K tiene que ser diferente de cero.Vectores ortogonales
Dos vectores son ortogonales o perpendiculares cuando forman ángulo recto entre sí. Si el producto escalar de dos vectores es cero, ambos vectores son ortogonalesya que el .
Vectores paralelos o en una misma dirección
Dos vectores son paralelos o llevan la misma dirección si el ángulo que forman es de 0 radianes (0 grados) o de π radianes (180 grados).Cuando dos vectores forman un ángulo cero, el valor del coseno es la unidad, por lo tanto el producto de los módulos vale lo mismo que el producto escalar.
Propiedades del producto escalar
Sean A, B y C vectores en el plano o en el espacio y sea m un escalar:
1. Conmutativa:
2. Distributiva respecto a la suma vectorial:
3. Asociatividad respecto al producto por un escalar m:
Expresión analítica del producto escalar
Si los vectores A y B se expresan en función de sus componentes cartesianas rectangulares, tomando la base canónica en formada por los vectores unitarios i , j , k tenemos:
El producto escalar se realiza como un producto matricial de la siguiente forma:
Así, generalizando para un espacio de n dimensiones
- si A y B son vectores o puntos en un espacio entonces:
- el producto escalar se realizaría como un producto matricial de la siguiente forma:
Norma o Módulo de un vector
Se define como la longitud del segmento orientado (vector) en el espacio métrico considerado.
Se calcula a través del producto interno del vector consigo mismo.
Efectuado el producto escalar, tenemos:
de modo que
Por componentes, tomando la base canónica en formada por los vectores unitarios {i, j, k}
de modo que
La componente de un vector a lo largo de un eje puede escribirse como el producto escalar del vector por el vector unitario sobre dicho eje. Por ejemplo la componente Ax se obtiene del producto:
A • i = (Axi + Ayj + Azk) • i = A
Esta relación sugiere un procedimiento algebraico para obtener una ecuación paras las componentes a partir de una ecuación vectorial. Multiplicando la ecuación vectorial A + B = C por i se obtiene A • i + B • i = C • i que conduce a Ax + Bx = Cx
Derivada del producto punto
Para establecer la regla de la diferenciación del producto escalar, diferenciamos ambos miembros de la ecuación:
A • B = AxBx + AyBy
d (A • B) =d (AxBx + AyBy) = dAx Bx + Ax dBx + dAy By+ Ay dBy
dt dt dt dt dt dt
reordenando y operando:
d (A • B) = dA • B + A • dB
dt dt dt
Diferenciación de un producto escalar por sí mismo, sea v el vector velocidad de modulo v y a es la aceleración.
d(v²) = d (v • v) = dv • v+ v • dv = 2 dv • v
dt dt dt dt dt
d (v²) =2a • v
dt
Potencia
La potencia P suministrada por una fuerza es el trabajo por unidad de tiempo que realiza dicha fuerza. Consideremos una partícula con velocidad instantánea v. En un intervalo corto de tiempo dt, la partícula se desplaza ds = v dt. El trabajo realizado por una fuerza F que actúa sobre la partícula durante ese intervalo de tiempo es:
dW = F • ds = F • v dt
La potencia suministrada por la partícula es
P = dW/dt = F • v
La unidad del SI de potencia, julio por segundo, se denomina (W)
1 W = 1 J /s
Observe la diferencia entre potencia y trabajo. Dos motores que elevan una determinada carga a igual distancia consumen la misma energía, pero el que lo levanta en menos tiempo es más potente.
Potencia y energía cinética
Demostraremos que la potencia transmitida sobre una partícula por la fuerza neta que actúa sobre ella se iguala con la tasa de cambio de la energía cinética de la partícula.
Como la potencia transmitida por la fuerza viene dada por Fneta • v. Demostraremos que Fneta • v = dEc/dt, donde Ec = ½mv²
Como
2a • v = d (v²)
dt
de F = ma tenemos que
2 Fneta • v
m
Fneta • v = m d (v²) = d (½ mv²)
2 dt dt
Pneta = d (½ mv²) = dEc
dt dt
Trabajo y energía en tres dimensiones
De lo anterior podemos establecer el Teorema trabajo - energía cinética en tres dimensiones, y puede establecerse integrando los dos términos de esta ecuación con respecto del tiempo. Esto nos conduce a:
t2 t2
∫Fneta • v dt = ∫(dEc/dt)dt
t1 t1
como ds = v dt, donde ds es el desplzamiento durante el tiempo dt, y teniendo en cuenta, además, que (dEc/dt)dt = dEc la ecuación anterior puede expresarse:
2 2
∫Fneta • ds = ∫dEc
1 1
en donde la integral de la izquierda es el trabajo total Wtotal realizado sobre la partícula. El primer miembro de la expresión anterior puede integrarse, lo cual lleva a
2
Wtotal = ∫Fneta • ds = Ec2 - Ec1 = ∆Ec
1
Energía potencial
La energía potencial es la energía mecánica asociada a la localización de un cuerpo dentro de un campo de fuerzas (gravitatoria, electrostática, etc.) o a existencia de un campo de fuerzas en el interior de un cuerpo (energía elástica). La energía potencial de un cuerpo es una consecuencia de la que el sistema de fuerzas que actúa sobre un cuerpo sea conservativo.
Independientemente de la fuerza que la origine, la energía potencial que posee el sistema físico representa la energía "almacenada" en virtud de su posición y/o configuración, por contraposición con la energía cinética que tiene y que representa su energía debida al movimiento. Para un sistema conservativo, la suma de energía cinética y potencial es constante, eso justifica el nombre de fuerzas conservativas, es decir, aquellas que hacen que la energía "se conserve". El concepto de energía potencial también puede usarse para sistemas físicos en los que intervienen fuerzas disipativas, y que por tanto no conservan la energía, sólo que en ese caso la energía mecánica total no será constante, y para aplicar el principio de conservación de la energía es necesario contabilizar la disipación de energía.1
El valor de la energía potencial depende siempre del punto o configuración de referencia escogido para medirla, por esa razón se dice a veces que físicamente sólo importa la variación de energía potencial entre dos configuraciones.2.
La energía potencial interviene como se ha mencionado en el principio de conservación de la energía y su campo de aplicación es muy general. Está presente no solo en la física clásica, sino también de la física relativista y física cuántica. El concepto se ha generalizado también a la física de partículas, donde se han llegado a utilizar potenciales complejos con el objeto de incluir también la energía disipada por el sistema.3
Fuerzas conservativas
Una fuerza es conservativa si el trabajo total que realiza sobre una partícula es cero, cuando la partícula recorre una trayectoria cerrada y vuelve a su posición inicial.
El trabajo realizado por una fuerza conservativa es independiente de la trayectoria seguida por la partícula cuando se mueve de un punto a otro.
Como el trabajo realizado por una fuerza conservativa sobre una partícula no depende de la trayectoria, sólo depende de los puntos 1 y 2. Podemos usar esta propiedad para definir la función energía potencial U, asociada a una fuerza conservativa. En general, la función energía potencial se define de tal modo que el trabajo realizado por una fuerza conservativa sea igual a la disminución de la función energía-potencial:
2
W = ∫F • ds = -∆U
1
2
∆U= U2 - U1 = - ∫F • ds
1
Energía potencial de un muelle
Otro ejemplo de una fuerza conservativa es la que ejerce un muelle estirado (o comprimido). Supongamos que tiramos de un bloque atado a un muelle y lo desplazamos de una posición x=0 (equilibrio) a otra x1.
El muelle realiza un trabajo negativo porque su fuerza se opone a la dirección del movimiento. Si ahora dejamos el bloque en libertad, el muelle realiza un trabajo positivo, al acelerar el bloque hacia su posición inicial. el trabajo total realizado por el muelle para mover el bloque hasta su posición inicial x = x1 y devolverlo luego a x=0 es cero, independientemente del valor de x1 (siempre que el alargamiento no supere el límite de elasticidad del muelle). La fuerza que ejerce el muelle es, por lo tanto, una fuerza conservativa.
Calculando la función energía potencial asociada a esta fuerza tenemos:
dU = -F ds = -Fx dx = -(-kx)dx = +kx dx
por lo tanto
U = ∫kx dx = ½ kx² + U0
U = ½ k x²
Cuando tiramos del bloque desde x=0 hasta x=x1, ejercemos una fuerza aplicada sobre el muelle. Si el bloque inicia su movimiento en x=0 y lo acaba en x=x1, en ambos casos en reposo, el cambio de su energía cinética es cero. El teorema trabajo-energía implica que el trabajo total realizado sobre el bloque es cero, es decir Wap + Wmuelle = 0
Wap = - Wmuelle = ∆Umuelle = ½ kx1² - 0 = ½ kx1²
Este trabajo se almacena en forma de energía potencial en el sistema muelle - bloque.
Fuerzas no conservativas
En contraposición, las fuerzas no conservativas son aquellas en las que el trabajo a lo largo de un camino cerrado es distinto de cero. Estas fuerzas realizan más trabajo cuando el camino es más largo, por lo tanto el trabajo no es independiente del camino.
No todas las fuerza con conservativas. Supongamos que se empuja desde un punto A hasta un punto B una caja situada encima de una mesa y luego se vuelve de B a A, de forma que la caja en el mismo sitio de donde ha salido. El rozamiento se opone al movimiento, por lo que la fuerza que se ejerce al empujar la caja, que siempre va en la dirección del movimiento, realiza un trabajo positivo en los dos tramos del trayecto. Por lo tanto, el trabajo total que ha hecho el empuje no es cero y nos encontramos ante un ejemplo de fuerza no conservativa para la cual no podemos definir una función energía potencial.
Energía potencial y equilibrio
Para una fuerza conservativa general en una dimensión, F = Fxi tenemos
dU = -F • ds = -Fx dx
La fuerza es, por tanto, la derivada negativa de la función energía potencial
Fx = -dU/dx
Esta expresión general puede comprobarse para el caso de un sistema bloque-muelle diferenciando la función U = ½ k x² , con lo que obtenemos
Fx = -dU/dx = d (½ k x² ) = -kx
dx
Una partícula está en equilibrio si la fuerza neta que actúa sobre ella es nula.




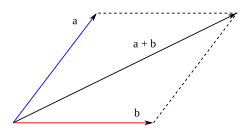
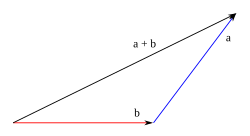





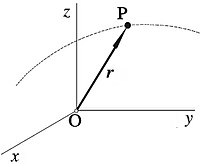

















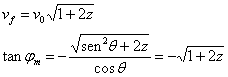




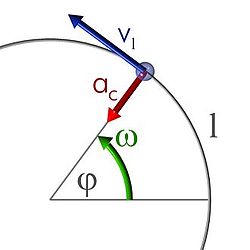






































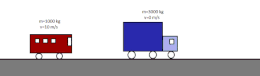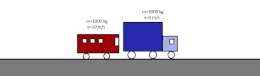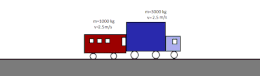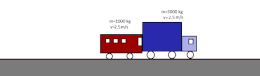







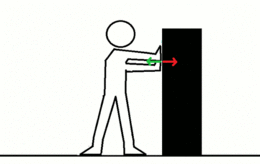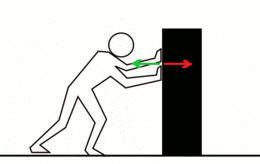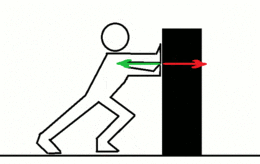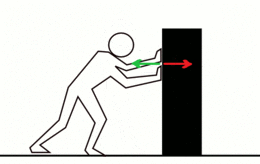
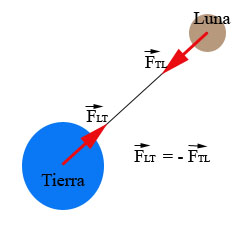
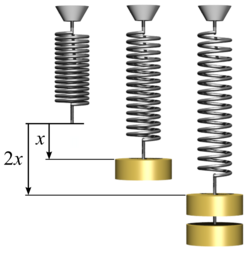














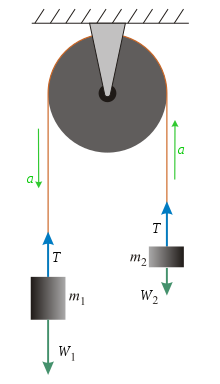















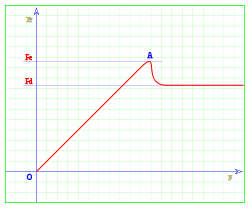









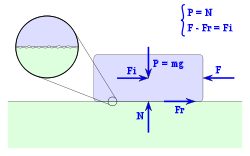





















































No hay comentarios.:
Publicar un comentario